Question

Construct a \[\Delta ABC\] in which \[AB = 4{\text{ cm}}\], \[BC = 5{\text{ cm}}\] and \[AC = 6{\text{ cm}}\]. Now, construct a triangle similar to \[\Delta ABC\] such that each of its sides is two-third of the corresponding sides of \[\Delta ABC\]. Also, prove your assertion.

Answer 1

Hint: First of all, construct the triangles by the given data by writing steps clearly. Then prove the formed triangles are congruent by using AA similarity criterion. So, use this concept to reach the solution of the given problem.

Complete step-by-step answer:
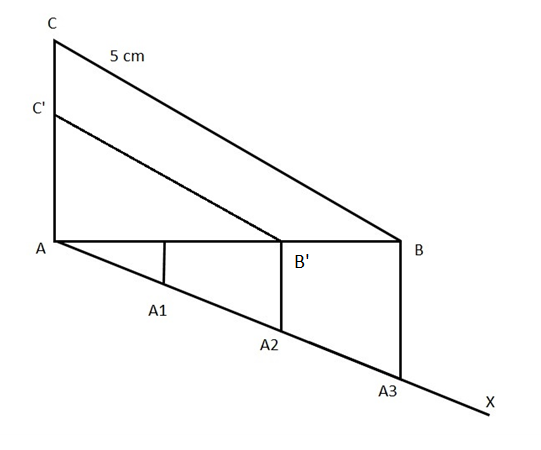
Steps for construction of the triangles:
1. Draw the base with \[AB = 4{\text{ cm}}\]
2. Draw an arc with A as centre, with a scale of 5 cm as radius.
3. Draw an arc with B as centre, with a scale of 6 cm as radius.
4. Let C be the point of intersection of the above 2 lines.
5. Draw a ray AX making an acute with line AB on the opposite side of the vertex is C.
6. Mark 3 points \[{A_1},{A_2}{\text{ and }}{A_3}\] such that \[{A_1}{A_2} = {A_2}{A_3} = {A_3}{A_1}\].
7. Join \[{A_3}B\] and draw a parallel line \[B'{A_2}\].
8. Draw a line parallel to BC to intersect AC at \[C'\].
Thus, the required triangle is \[AB'C'\]

Justification:
By construction, we have
\[\dfrac{{AB'}}{{AB}} = \dfrac{{A{A_2}}}{{A{A_3}}} = \dfrac{2}{3}.......................................................\left( 1 \right)\]
And also \[B'C'\parallel BC\]
Therefore, \[\angle AB'C' = \angle ABC\]
In \[\Delta ABC\] and \[\Delta AB'C'\], we have
\[
  \angle A = \angle A{\text{ }}\left( {{\text{Common angles}}} \right) \\
  \angle AB'C' = \angle ABC{\text{ }}\left( {{\text{Angle property of parallel lines}}} \right) \\
\]
Thus, by AA similarity criterion \[\Delta ABC \sim \Delta AB'C'\].
We know that in similar triangles, the sides are in common ratio.
So, \[\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}} = \dfrac{{B'C'}}{{BC}}\]
Therefore, \[\dfrac{{AB'}}{{AB}} = \dfrac{{AC'}}{{AC}} = \dfrac{{B'C'}}{{BC}} = \dfrac{2}{3}{\text{ }}\left( {{\text{Using }}\left( 1 \right)} \right)\]
Hence the assertion is proved.

Note: The AA criterion tells us that two triangles are similar if two corresponding angles are equal to each other. The angle property of parallel lines tells us that if two parallel lines are cut by a transversal, the corresponding angles are congruent.