Question

Construct a circle of radius 3.5cm and construct a central angle of measure $80{}^\circ $ and an inscribed angle subtended by the same arc. Construct tangents at the endpoints of the arc and extend them to intersect each other. Comment your observations

Answer 1

Hint: Tangent to a circle forms a right angle with the radius at the point of contact. Hence when drawing tangent at a point on the circle, join the centre of the circle with the point and draw a line perpendicular to that line passing through the given point. The line hence constructed will be tangent to the circle.

Complete step-by-step answer:

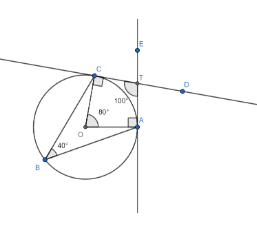
The constructed figure is as shown above.
Steps of Construction:
[1] Mark a point O on the paper.
[2] With O as centre and radius OP = 3.5cm draw a circle.
[3] Mark any point A on the circle.
[4] Using a protractor construct an angle of $80{}^\circ $ on the line OA and let the other arm of the angle meet the circle at point C.
[5] Mark any point B in the alternate segment.
[6] Join CB and AB. $\angle \text{CBA}$ is an inscribed angle subtended by the minor arc $\overset\frown{AC}$ .
[7] Draw $\angle \text{DCO=90}{}^\circ $ and $\angle \text{EAO=90}{}^\circ $ . Let DC and EA meet at point T.
[8] Hence TA and TC are the tangents at the points of the minor arc $\overset\frown{AC}$ .
[9] measure $\angle \text{CBA}$ and $\angle \text{CTA}$
Observations: $\angle \text{CBA=40}{}^\circ \text{=}\dfrac{1}{2}\angle \text{COA}$ and $\angle \text{CTA=180}{}^\circ \text{-}\angle \text{COA}$.
[a] Hence the angle subtended by an arc in the alternate segment is half the angle subtended by the arc at the centre of the circle.
[b] If tangents at any two points A and B of a circle with centre O meet at T, then TAOC is a cyclic quadrilateral. TAOC is also a kite.
Note: [1] Angle subtended by an arc at the centre of a circle is twice the angle subtended by the arc in the alternate segment.

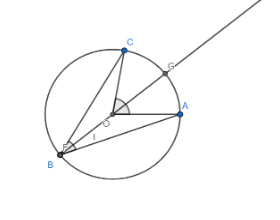
Hence from the diagram above, we have $\angle \text{COA=2}\angle \text{CBA}$
Proof:
In the triangle COB, $\angle \text{COG}$ is an exterior angle.
So, we have
$\angle \text{COG=}\angle \text{CBO+}\angle \text{BCO }\left\{ \because \text{exterior angle property} \right\}$
Since OB = OC {radii of the same circle},
So, we have $\angle \text{CBO=}\angle \text{BCO}$
Hence $\angle \text{COG=2}\angle \text{CBO (i)}$
Similarly $\angle \text{AOG=2}\angle \text{ABO (ii)}$
Adding equation (i) and equation (ii), we get
$\begin{align}
  & \angle \text{AOG+}\angle \text{COG=2}\angle \text{ABO+2}\angle \text{CBO} \\
 & \Rightarrow \angle \text{COA=2}\angle \text{CBA} \\
\end{align}$
Hence proved.
[2] If tangents at any two points A and B of a circle with centre O meet at T, then TAOC is a cyclic quadrilateral. TAOC is also a kite.

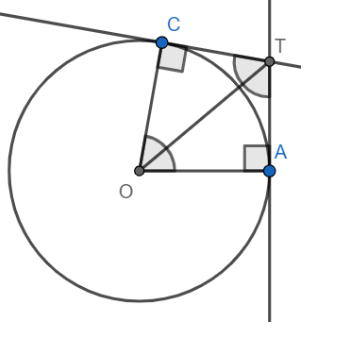
Proof:
Since CT is tangent to the circle, we have $\text{CT}\bot \text{OC}$
Similarly $\text{OA}\bot \text{AT}$
Hence $\angle \text{OCT+}\angle \text{OAT=90}{}^\circ \text{+90}{}^\circ \text{=180}{}^\circ $
Applying angle sum property in quadrilateral TAOC, we get
$\angle \text{CTA+}\angle \text{COA=180}{}^\circ $
Hence TAOC is a cyclic quadrilateral.
Also in triangle OAT and OCT, we have
$\angle \text{OAT=}\angle \text{OCT}$ (each 90)
OT = OT (common side)
OA = OC (radii of the same circle)
Hence $\Delta \text{OAT}\cong \Delta \text{OCT by RHS congruency}$
Hence OA = OC and AT = CT (corresponding parts of congruent triangles)
Hence TAOC is a kite.