Question

Consider two different metallic strips (1 and 2) of same dimensions (length l, width w and thickness d) with carrier densities ${n_1}$ and ${n_2}$ respectively. Strip 1 is placed in magnetic field ${B_1}$ and strip 2 is placed in the magnetic field ${B_2}$ , both along positive y-directions. Then ${V_1}$ and ${V_2}$ are potential difference developed between K and M in strips 1 and 2 respectively:

Answer 1

Hint: In this question, we will use the relation between the two potential differences, magnetic field and the carrier densities. Further, by applying different conditions we will get the required answer. Also,we will study the basics of magnetic field and the two rules to find the direction of magnetic field, for our better understanding.
Formula used:
$\dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{{B_2}}}{{{B_1}}}\dfrac{{{n_1}}}{{{n_2}}}$

Complete answer:
As we know that, potential difference can be defined as the difference in potential between the two points that represent the work involved or we can say, the energy released in the transfer of a unit quantity of electricity from one point to the other.
As we know, the ratio of potential difference is given by:
$\dfrac{{{V_2}}}{{{V_1}}} = \dfrac{{{B_2}}}{{{B_1}}}\dfrac{{{n_1}}}{{{n_2}}}.........(1)$
From the question, we have:
${B_1} = {B_2}$
${n_1} = 2{n_2}$
Substituting these values in equation (1), we get:
$\therefore {V_2} = 2{V_1}$
Further, we also have:
${B_1} = 2{B_2}$
${n_1} = {n_2}$
Now, substituting these values in equation (1), we get:
$\therefore {V_2} = 0.5{V_1}$
Therefore, we get the required answer; here we have two values of the potential difference, in two different conditions.

Additional information:
A magnetic field B can be defined as a vector field that tells the magnetic influence on moving electric charges, electric currents, and magnetized materials. Also, we should know that a charge that is moving in a magnetic field experiences a force that is perpendicular to its town velocity and to the magnetic field.
Fleming's left-hand rule is used to find the direction of magnetic force acting in electric motors. We know that an electric current and magnetic field exist in an electric motor, and these lead to the force that creates the motion.

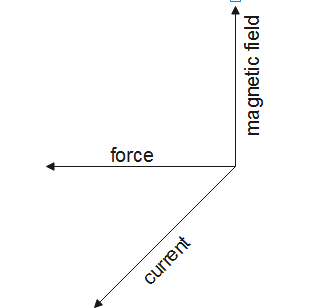
 So, the left hand rule is used here which gives the direction of magnetic force acting in the electric motor.
Fleming's right-hand rule is used to find the direction of induced current in an electric generator. As we know that in an electric generator, the motion and magnetic field exist and these lead to the production of an electric current in the generator.
 

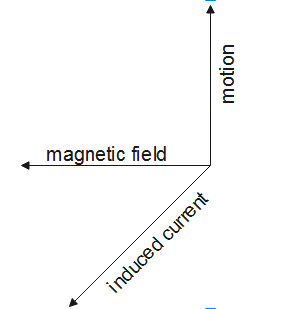
So, the right hand rule is used here to find the direction of induced current in an electric generator.

Note:
Do remember that potential difference is measured in Joule per coulomb. Also, note the rules because both the rules tell the different fields. Further, we need to notice the direction of the magnetic field i.e., whether the field is inward or outward. All the three fingers should be placed perpendicular to each other.