
Consider the three statements :
(i) In a $\Delta ABC,AD$ is a median. Prove that $A{{B}^{2}}+A{{C}^{2}}=2A{{D}^{2}}+2D{{C}^{2}}$.
(ii) In a $\Delta ABC,\angle ABC={{135}^{\circ }}$. Prove that $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+4ar\left( \Delta ABC \right)$.
(iii) In a quadrilateral $ABCD,\angle B={{90}^{\circ }}$. If $A{{D}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}$, then prove that $\angle ACD={{90}^{\circ }}$.
Answer
577.2k+ views
Hint: For statement (i), draw a rough diagram of the given condition. Join a perpendicular line segment AM from point A on side BC. Use Pythagoras theorem given as ${{h}^{2}}={{b}^{2}}+{{p}^{2}}$, where h = hypotenuse, b = base and p = perpendicular to prove the given relation.
For statement (ii), apply cosine rule in a triangle given as : $\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$, where a, b, and c are the sides opposite to angles A, B and C respectively. Substitute the value of A equal to ${{135}^{\circ }}$ and use the area relation : Area of triangle = $\dfrac{1}{2}bc\sin A$, to get the required proof.
For statement (iii), use the converse of Pythagoras theorem, in the rough diagram of quadrilateral, given as : ‘if the sum of squares of two sides of a triangle is equal to the square of third side, then the triangle is right triangle’, Apply the above theorem to get the required proof.
Complete step by step answer:
Now, here, we have been provided with three statements and we have to prove them. So, let us check them one by one.
(i) Here, we have to prove $A{{B}^{2}}+A{{C}^{2}}=2A{{D}^{2}}+2D{{C}^{2}}$, given that AD is the median of the triangle ABC.
First let us draw a rough diagram of the given situation.
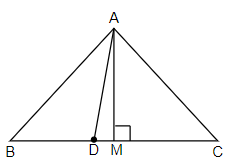
In the above figure we have considered AM perpendicular to BC so that we can apply Pythagoras theorem : ${{h}^{2}}={{b}^{2}}+{{p}^{2}}$ where h = hypotenuse, b = base and p = perpendicular. Now, we have,
$L.H.S=A{{B}^{2}}+A{{C}^{2}}\ldots \ldots \ldots \left( i \right)$
In $\Delta ABM$, we have,
$\begin{align}
& A{{B}^{2}}=A{{M}^{2}}+B{{M}^{2}} \\
& \Rightarrow A{{B}^{2}}=A{{M}^{2}}+{{\left( BD+DM \right)}^{2}} \\
& \Rightarrow A{{B}^{2}}=A{{M}^{2}}+B{{D}^{2}}+D{{M}^{2}}+2BD.DM \\
\end{align}$
Since, AD is the median, therefore BD = CD.
$\Rightarrow A{{B}^{2}}=A{{M}^{2}}+C{{D}^{2}}+D{{M}^{2}}+2CD.DM$
In $\Delta ACM$, we have,
$\begin{align}
& A{{C}^{2}}=A{{M}^{2}}+C{{M}^{2}} \\
& \Rightarrow A{{C}^{2}}=A{{M}^{2}}+{{\left( CD-DM \right)}^{2}} \\
& \Rightarrow A{{C}^{2}}=A{{M}^{2}}+C{{D}^{2}}+D{{M}^{2}}-2CD.DM \\
\end{align}$
Now, substituting the value of $A{{B}^{2}}$ and $A{{C}^{2}}$ in equation (i), we get,
$\begin{align}
& L.H.S=\left( A{{M}^{2}}+C{{D}^{2}}+D{{M}^{2}}+2CD.DM \right)+\left( A{{M}^{2}}+C{{D}^{2}}+D{{M}^{2}}-2CD.DM \right) \\
& \Rightarrow 2A{{M}^{2}}+2C{{D}^{2}}+2D{{M}^{2}} \\
\end{align}$
In right angle triangle AMD, we have,
$\begin{align}
& A{{M}^{2}}+D{{M}^{2}}=A{{D}^{2}} \\
& \Rightarrow L.H.S=2\left( A{{M}^{2}}+D{{M}^{2}} \right)+2C{{D}^{2}} \\
& =2A{{D}^{2}}+2C{{D}^{2}} \\
& =R.H.S \\
\end{align}$
Hence, proved.
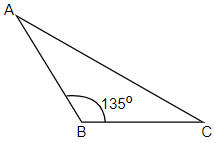
(ii) Here, we have been given, in a $\Delta ABC,\angle ABC={{135}^{\circ }}$ and we have to prove that $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+4ar\left( \Delta ABC \right)$. SO, let us draw a rough diagram for the given situation.
Now, we know that in a triangle represented with sides a, b and c opposite to the angles A, B and C, we have,
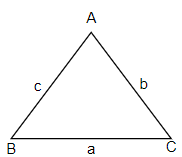
$\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
This is called cosine formula. So, applying in the triangle drawn for the question, we get,
$\cos B=\dfrac{A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}}{2AB.BC}$
Substituting $B={{135}^{\circ }}$, we get,
$\begin{align}
& \cos {{135}^{\circ }}=\dfrac{A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}}{2AB.BC} \\
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=2AB.BC\cos {{135}^{\circ }} \\
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=2AB.BC\cos \left( {{90}^{\circ }}+{{45}^{\circ }} \right) \\
\end{align}$
We know that $\cos \left( {{90}^{\circ }}+{{45}^{\circ }} \right)=-\sin {{45}^{\circ }}$, therefore, we have,
$\Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=-2AB.BC\sin {{45}^{\circ }}\ldots \ldots \ldots \left( ii \right)$
We know that area of triangle ABC is given as :
Area = $\dfrac{1}{2}ab\sin C$
= $\dfrac{1}{2}bc\sin A$
= $\dfrac{1}{2}ac\sin B$
Therefore, using Area = $\dfrac{1}{2}ac\sin B$ and substituting $B={{135}^{\circ }}$, we get,
$\begin{align}
& Area.\left( \Delta ABC \right)=\dfrac{1}{2}AB.BC\sin {{135}^{\circ }} \\
& \Rightarrow Ar.\left( \Delta ABC \right)=\dfrac{1}{2}AB.BC\sin \left( {{180}^{\circ }}-{{45}^{\circ }} \right) \\
\end{align}$
We know that $\sin \left( {{180}^{\circ }}-{{45}^{\circ }} \right)=\sin {{45}^{\circ }}$
$\Rightarrow Ar.\left( \Delta ABC \right)=\dfrac{1}{2}AB.BC\sin {{45}^{\circ }}$
Substituting the above value in equation (ii), we have,
$\begin{align}
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=-2\times 2Ar.\left( \Delta ABC \right) \\
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=-4Ar.\left( \Delta ABC \right) \\
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}+4Ar.\left( \Delta ABC \right)=A{{C}^{2}} \\
& \Rightarrow A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+4Ar.\left( \Delta ABC \right) \\
& \Rightarrow L.H.S=R.H.S \\
\end{align}$
Hence, proved.
(iii) here, we have been provided with a quadrilateral ABCD with $\angle B={{90}^{\circ }}$ and $A{{D}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}$. We have to prove $\angle ACD={{90}^{\circ }}$. Let us draw a rough diagram of the given condition.
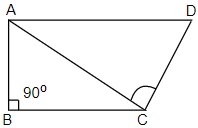
$\because A{{D}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}\ldots \ldots \ldots \left( iii \right)$
Now, in right angle triangle ABC, using Pythagoras Theorem, we get,
$A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$
Therefore, substituting this value in equation (iii), we get,
$\begin{align}
& \Rightarrow A{{D}^{2}}=A{{C}^{2}}+C{{D}^{2}} \\
& \Rightarrow A{{C}^{2}}+C{{D}^{2}}=A{{D}^{2}} \\
\end{align}$
So, in triangle ACD, we have $A{{C}^{2}}+C{{D}^{2}}=A{{D}^{2}}$, so applying the converse of Pythagoras theorem given by the statement : ‘if the sum of squares of two sides of a triangle is equal to the square of third side’, we get,
$\Delta ACD$ is a right angle triangle at $\angle ACD$. Therefore, we can say that, $\angle ACD={{90}^{\circ }}$.
Hence, proved.
Note: One must remember the use of Pythagoras theorem to solve the above three questions. You may note that the cosine formula we have used in proving statement (ii) is also derived by using the Pythagoras theorem. You must remember the three area relations of a triangle given in terms of sine of the angles. If we will use the basic formula for area of triangle in statement (ii) then it will be a lengthy process because then we will have to perform some constructions.
For statement (ii), apply cosine rule in a triangle given as : $\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$, where a, b, and c are the sides opposite to angles A, B and C respectively. Substitute the value of A equal to ${{135}^{\circ }}$ and use the area relation : Area of triangle = $\dfrac{1}{2}bc\sin A$, to get the required proof.
For statement (iii), use the converse of Pythagoras theorem, in the rough diagram of quadrilateral, given as : ‘if the sum of squares of two sides of a triangle is equal to the square of third side, then the triangle is right triangle’, Apply the above theorem to get the required proof.
Complete step by step answer:
Now, here, we have been provided with three statements and we have to prove them. So, let us check them one by one.
(i) Here, we have to prove $A{{B}^{2}}+A{{C}^{2}}=2A{{D}^{2}}+2D{{C}^{2}}$, given that AD is the median of the triangle ABC.
First let us draw a rough diagram of the given situation.

In the above figure we have considered AM perpendicular to BC so that we can apply Pythagoras theorem : ${{h}^{2}}={{b}^{2}}+{{p}^{2}}$ where h = hypotenuse, b = base and p = perpendicular. Now, we have,
$L.H.S=A{{B}^{2}}+A{{C}^{2}}\ldots \ldots \ldots \left( i \right)$
In $\Delta ABM$, we have,
$\begin{align}
& A{{B}^{2}}=A{{M}^{2}}+B{{M}^{2}} \\
& \Rightarrow A{{B}^{2}}=A{{M}^{2}}+{{\left( BD+DM \right)}^{2}} \\
& \Rightarrow A{{B}^{2}}=A{{M}^{2}}+B{{D}^{2}}+D{{M}^{2}}+2BD.DM \\
\end{align}$
Since, AD is the median, therefore BD = CD.
$\Rightarrow A{{B}^{2}}=A{{M}^{2}}+C{{D}^{2}}+D{{M}^{2}}+2CD.DM$
In $\Delta ACM$, we have,
$\begin{align}
& A{{C}^{2}}=A{{M}^{2}}+C{{M}^{2}} \\
& \Rightarrow A{{C}^{2}}=A{{M}^{2}}+{{\left( CD-DM \right)}^{2}} \\
& \Rightarrow A{{C}^{2}}=A{{M}^{2}}+C{{D}^{2}}+D{{M}^{2}}-2CD.DM \\
\end{align}$
Now, substituting the value of $A{{B}^{2}}$ and $A{{C}^{2}}$ in equation (i), we get,
$\begin{align}
& L.H.S=\left( A{{M}^{2}}+C{{D}^{2}}+D{{M}^{2}}+2CD.DM \right)+\left( A{{M}^{2}}+C{{D}^{2}}+D{{M}^{2}}-2CD.DM \right) \\
& \Rightarrow 2A{{M}^{2}}+2C{{D}^{2}}+2D{{M}^{2}} \\
\end{align}$
In right angle triangle AMD, we have,
$\begin{align}
& A{{M}^{2}}+D{{M}^{2}}=A{{D}^{2}} \\
& \Rightarrow L.H.S=2\left( A{{M}^{2}}+D{{M}^{2}} \right)+2C{{D}^{2}} \\
& =2A{{D}^{2}}+2C{{D}^{2}} \\
& =R.H.S \\
\end{align}$
Hence, proved.
(ii) Here, we have been given, in a $\Delta ABC,\angle ABC={{135}^{\circ }}$ and we have to prove that $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+4ar\left( \Delta ABC \right)$. SO, let us draw a rough diagram for the given situation.

Now, we know that in a triangle represented with sides a, b and c opposite to the angles A, B and C, we have,

$\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$
This is called cosine formula. So, applying in the triangle drawn for the question, we get,
$\cos B=\dfrac{A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}}{2AB.BC}$
Substituting $B={{135}^{\circ }}$, we get,
$\begin{align}
& \cos {{135}^{\circ }}=\dfrac{A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}}{2AB.BC} \\
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=2AB.BC\cos {{135}^{\circ }} \\
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=2AB.BC\cos \left( {{90}^{\circ }}+{{45}^{\circ }} \right) \\
\end{align}$
We know that $\cos \left( {{90}^{\circ }}+{{45}^{\circ }} \right)=-\sin {{45}^{\circ }}$, therefore, we have,
$\Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=-2AB.BC\sin {{45}^{\circ }}\ldots \ldots \ldots \left( ii \right)$
We know that area of triangle ABC is given as :
Area = $\dfrac{1}{2}ab\sin C$
= $\dfrac{1}{2}bc\sin A$
= $\dfrac{1}{2}ac\sin B$
Therefore, using Area = $\dfrac{1}{2}ac\sin B$ and substituting $B={{135}^{\circ }}$, we get,
$\begin{align}
& Area.\left( \Delta ABC \right)=\dfrac{1}{2}AB.BC\sin {{135}^{\circ }} \\
& \Rightarrow Ar.\left( \Delta ABC \right)=\dfrac{1}{2}AB.BC\sin \left( {{180}^{\circ }}-{{45}^{\circ }} \right) \\
\end{align}$
We know that $\sin \left( {{180}^{\circ }}-{{45}^{\circ }} \right)=\sin {{45}^{\circ }}$
$\Rightarrow Ar.\left( \Delta ABC \right)=\dfrac{1}{2}AB.BC\sin {{45}^{\circ }}$
Substituting the above value in equation (ii), we have,
$\begin{align}
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=-2\times 2Ar.\left( \Delta ABC \right) \\
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}-A{{C}^{2}}=-4Ar.\left( \Delta ABC \right) \\
& \Rightarrow A{{B}^{2}}+B{{C}^{2}}+4Ar.\left( \Delta ABC \right)=A{{C}^{2}} \\
& \Rightarrow A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}+4Ar.\left( \Delta ABC \right) \\
& \Rightarrow L.H.S=R.H.S \\
\end{align}$
Hence, proved.
(iii) here, we have been provided with a quadrilateral ABCD with $\angle B={{90}^{\circ }}$ and $A{{D}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}$. We have to prove $\angle ACD={{90}^{\circ }}$. Let us draw a rough diagram of the given condition.

$\because A{{D}^{2}}=A{{B}^{2}}+B{{C}^{2}}+C{{D}^{2}}\ldots \ldots \ldots \left( iii \right)$
Now, in right angle triangle ABC, using Pythagoras Theorem, we get,
$A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}}$
Therefore, substituting this value in equation (iii), we get,
$\begin{align}
& \Rightarrow A{{D}^{2}}=A{{C}^{2}}+C{{D}^{2}} \\
& \Rightarrow A{{C}^{2}}+C{{D}^{2}}=A{{D}^{2}} \\
\end{align}$
So, in triangle ACD, we have $A{{C}^{2}}+C{{D}^{2}}=A{{D}^{2}}$, so applying the converse of Pythagoras theorem given by the statement : ‘if the sum of squares of two sides of a triangle is equal to the square of third side’, we get,
$\Delta ACD$ is a right angle triangle at $\angle ACD$. Therefore, we can say that, $\angle ACD={{90}^{\circ }}$.
Hence, proved.
Note: One must remember the use of Pythagoras theorem to solve the above three questions. You may note that the cosine formula we have used in proving statement (ii) is also derived by using the Pythagoras theorem. You must remember the three area relations of a triangle given in terms of sine of the angles. If we will use the basic formula for area of triangle in statement (ii) then it will be a lengthy process because then we will have to perform some constructions.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




