Question

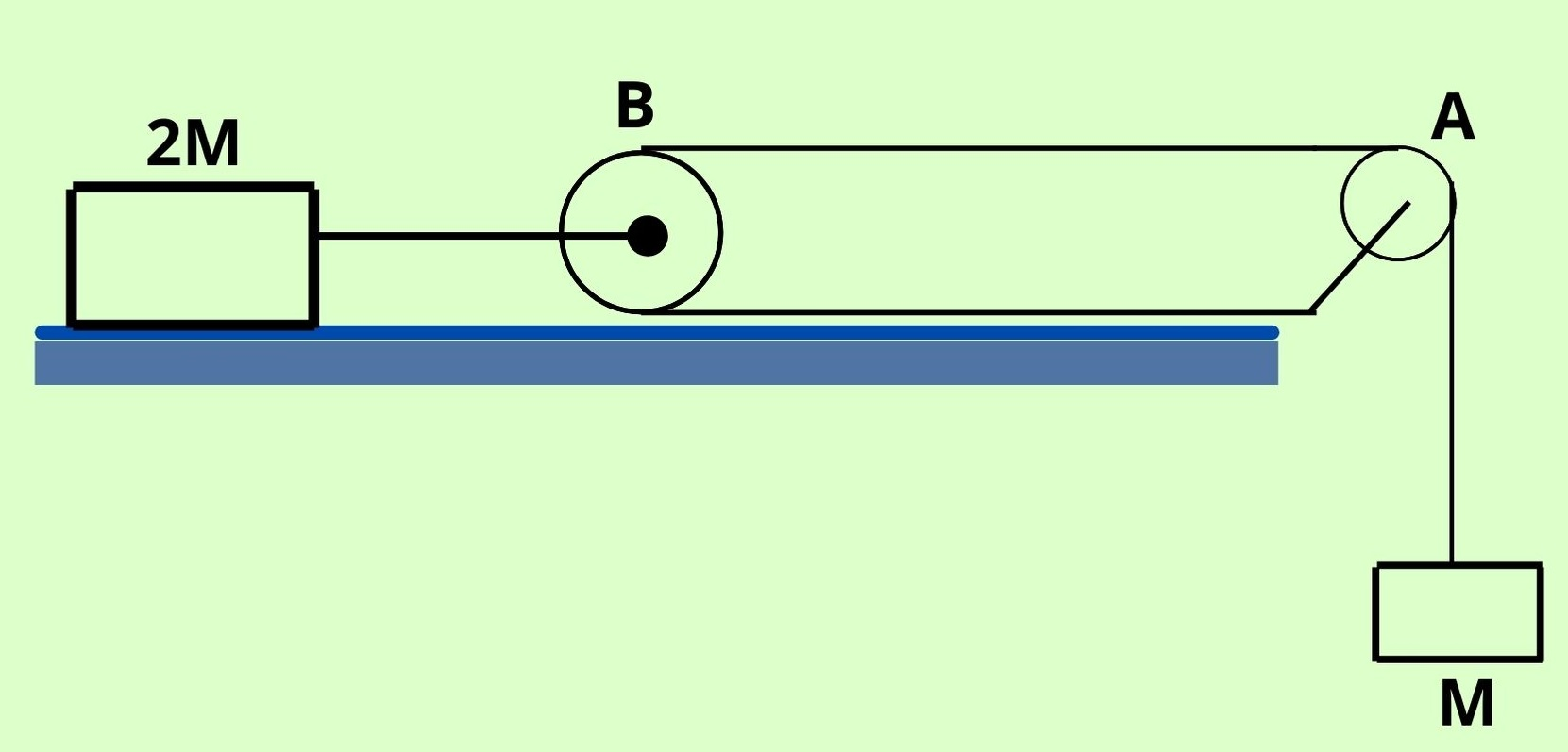
Consider the situation in figure. Both the pulleys and the string are light and all the surfaces are frictionless. Calculate the force exerted by the clamp on the pulley A in the figure.

Answer 1

Hint: The above problem can be solved by using the equilibrium equations of the forces in the given system. The hanged mass exerts the tension in the string. Both the strings between the pulley A and pulley B also remain under the tension in both strings. The block on the table starts moving if the effect of the tension in both strings becomes more than the force of the block.

Complete step by step solution:
Given: The mass of the hanging block is M, mass of the block on the table is 2 M.
The force on the block on the table is given as:
$T + T = Ma$
$2T = Ma$
$T = \dfrac{{Ma}}{2}$
The equilibrium equation for horizontal equilibrium is given as:
$T + Ma - Mg = 0......\left( 1 \right)$
Substitute all the values in the above expression.
$\dfrac{{Ma}}{2} + Ma - Mg = 0$
$\dfrac{{3Ma}}{2} = Mg$
$a = \dfrac{{2g}}{3}$
The resultant force exerted by the clamp on the pulley A is given as:
$F = \sqrt 2 T$
Substituting all the values in the above expression.
$F = \sqrt 2 \left( {Ma} \right)$
$F = \sqrt 2 M\left( {\dfrac{{2g}}{3}} \right)$
On simplification, we get
$F = \dfrac{{2\sqrt 2 Mg}}{3}$
Therefore, the resultant force exerted by the clamp on the pulley A is $\dfrac{{2\sqrt 2 Mg}}{3}$.

Additional Information:
The resultant tension of the both strings at the pulley A is obtained by the horizontal and vertical components of the tension acting on the pulley A.

Note: The tension arises in the string due to the weight of the hanging mass in downward direction. The object remains in the equilibrium conditions if the net forces in horizontal and vertical direction become zero.