Question

Consider the circle of radius 5 centered at (0, 0), how do you find an equation of the line tangent to the circle at the point (3, 4)?

Answer 1

Hint: Write the standard equation of the circle given as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where (a, b) is the coordinate of the center of the circle and r is radius of the circle. Substitute the given values to get the equation of the circle. Now, differentiate the obtained equation with respect to x and find the value of $\dfrac{dy}{dx}$ at (3, 4) which is the slope of the tangent. Finally, write the equation of the tangent line as $\left( y-{{y}_{1}} \right)=\dfrac{dy}{dx}\left( x-{{x}_{1}} \right)$ and simplify it to get the answer. Here, $\left( {{x}_{1}},{{y}_{1}} \right)=\left( 3,4 \right)$.

Complete step-by-step answer:
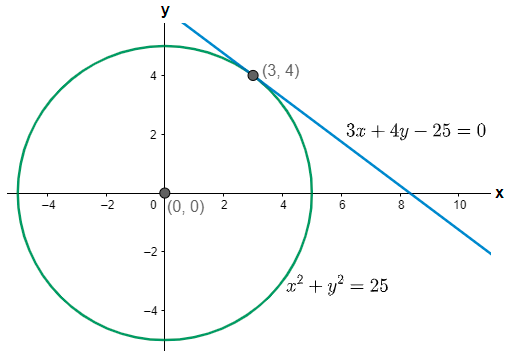
Here we have been provided with a circle of radius 5 units and whose center lies on the origin. We are asked to find the equation of a tangent line touching the circle at the point (3, 4).
Now, we know that the equation of a circle in standard form is given as ${{\left( x-a \right)}^{2}}+{{\left( y-b \right)}^{2}}={{r}^{2}}$ where (a, b) is the coordinate of the center of the circle and r is radius of the circle. Since, the center lies on the origin and radius is 5 units so we have (a, b) = (0, 0) and r = 5. Substituting the values in the equation of the circle we get,
$\begin{align}
  & \Rightarrow {{\left( x \right)}^{2}}+{{\left( y \right)}^{2}}={{5}^{2}} \\
 & \Rightarrow {{x}^{2}}+{{y}^{2}}=25 \\
\end{align}$
Now, we need to find the slope of the tangent at point (3, 4), so differentiating the above equation with respect to x we get,
 $\Rightarrow \dfrac{d\left( {{x}^{2}} \right)}{dx}+\dfrac{d\left( {{y}^{2}} \right)}{dx}=\dfrac{d\left( 25 \right)}{dx}$
We know that the derivative of a constant is 0. Also using the chain rule of derivative to differentiate ${{y}^{2}}$ we get,
$\begin{align}
  & \Rightarrow 2x+2y\dfrac{dy}{dx}=0 \\
 & \Rightarrow \dfrac{dy}{dx}=\dfrac{-x}{y} \\
\end{align}$
Therefore at point (3, 4) we have the slope of tangent given as: -
$\begin{align}
  & \Rightarrow 2x+2y\dfrac{dy}{dx}=0 \\
 & \Rightarrow \dfrac{dy}{dx}=\dfrac{-3}{4} \\
\end{align}$
We know that the equation of a line passing through the point $\left( {{x}_{1}},{{y}_{1}} \right)$ and having slope $\dfrac{dy}{dx}$ is given as $\left( y-{{y}_{1}} \right)=\dfrac{dy}{dx}\left( x-{{x}_{1}} \right)$, so we get,
$\Rightarrow \left( y-4 \right)=\dfrac{-3}{4}\left( x-3 \right)$
On simplifying we get,
\[\begin{align}
  & \Rightarrow 4y-16=-3x+9 \\
 & \therefore 3x+4y-25=0 \\
\end{align}\]
Hence, the above linear equation is the equation of the required tangent.

Note: Remember the equations of a circle in different forms like standard form, general form, polar form etc. An important form of a circle is given as ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ where $\left( -g,-f \right)$ is the center of the circle and $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ is the radius. Remember the basic rules of derivatives like the product rule, chain rule, $\dfrac{u}{v}$ rule etc. as they are frequently used in coordinate geometry and calculus.