Question

Consider for any three sets A, B and C, then $A\cap \left( B\cup C \right)$ is:
(a) $\left( A\cup B \right)\cap \left( B\cap C \right)$
(b) $\left( A\cap B \right)\cup \left( A\cap C \right)$
(c) $A\cup \left( B\cap C \right)$
(d) $\left( A\cup B \right)\cap \left( B\cup C \right)$

Answer 1

Hint:First try to draw a Venn diagram and get to a result. Take 3 sets A, B, C as examples. Substitute in the relation you got by using the Venn diagrams. By that you can verify your relation.

Complete step-by-step answer:
Venn diagrams: A Venn diagram is a diagram that shows all possible logical relations between the set of different sets. These diagrams depict elements as points in the space, and set as regions inside the closed curves which generally circles. Each circle represents a set. The overlapping region represents the common points between the sets.
Intersection of sets: In mathematics, intersection of 2 sets A, B is the set containing all elements common in both regions A, B denoted by $A\cap B$
Union of sets: In mathematics union of 2 sets A, B is the set containing all the elements belonging to A, B denoted by $A\cup B$
Given expression in the question: $A\cap \left( B\cup C \right)$
$B\cup C:$ This implies a region covered by B and C. So we must shade the whole region of circles B, C as shown in the figure.

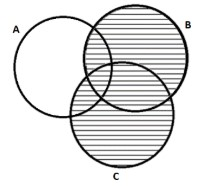
$\Rightarrow B\cup C$
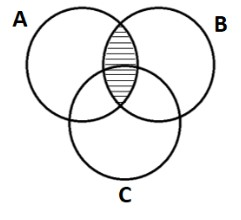
$A\cap \left( B\cup C \right):$ This is the diagram of region which is common to circle A and the shaded region from the previous figure. By this we get the following figure:

$\Rightarrow A\cap \left( B\cup C \right)$
Similarly as above we can say,
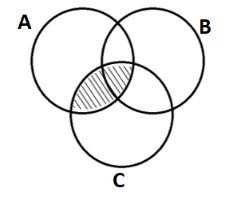
$A\cap B$: The region common to A, B circles is shaded.
By doing above, we get figure as:

$\Rightarrow A\cap B$
$A\cap C:$ The region common to A, C circles is shaded.
By doing above, we get figure as:

$\Rightarrow A\cap C$
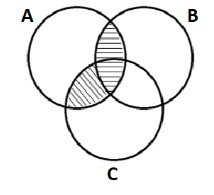
$\left( A\cap B \right)\cup \left( A\cap C \right):$ This region is nothing but the addition above previous 2 regions
By doing above, we get the diagram as below:

$\Rightarrow \left( A\cap B \right)\cup \left( A\cap C \right)$
So, by looking at all diagrams we can see the two diagrams are equal. So, we say:
 \[A\cap \left( B\cup C \right)=\left( A\cap B \right)\cup \left( A\cap C \right)\]
Now let us prove the same by taking examples:
Now let us assume, A = {1, 2, 3, 4, 5, 6}, B = {1, 2}, C = {5, 6}
$B\cup C$ = all elements in B, C = {1, 2, 5, 6}
$A\cap \left( B\cup C \right)$ = elements in A, $B\cup C$ = {1, 2, 5, 6}
$A\cap B$ = element in A, B = {1, 2} $A\cap C$ = {5, 6}
$\left( A\cap B \right)\cup \left( A\cap C \right)=\{1,2,5,6\}$
$\Rightarrow A\cap \left( B\cup C \right)=\left( A\cap B \right)\cup \left( A\cap C \right)$
We got answers by the Venn diagram method. We also justified it by proving with an example method. So, our answer is absolutely correct. We already justified it by our example.
Therefore option (b) is correct for the given expression in the question.

Note: While taking intersection and union in Venn diagram you must take care of the difference in their definitions as many students confuse this step. Any time to prove 2 expressions are equal the proof will be solid if we prove algebraically and then justify it with an example. Be careful while taking an example. Take an example such that A, B, C have some elements in common else intersection will be null set. So, it will become hard to justify.Students should remember the distributive and commutative property of sets.