Question

Consider a planet moving in an elliptical orbit around the Sun. The work done on the planet by the gravitational force of the Sun.
This question has multiple correct options
A. Is zero in any small part of the orbit
B. Is zero in some parts of the orbit
C. Is zero in complete revolution
D. Is zero in no part of the motion

Answer 1

Hint- This is the essential question of chapter gravitation. In some parts of the orbit, force is perpendicular to the direction of motion. Hence, no work done when rotating in circular orbits. Also the total amount of labor in the complete revolution is zero. Because when moving away the component of gravity is opposite to the direction of motion So, negative work is completed. In some parts positive work is completed. As both are symmetrical total work done is zero.

Complete step-by-step answer:

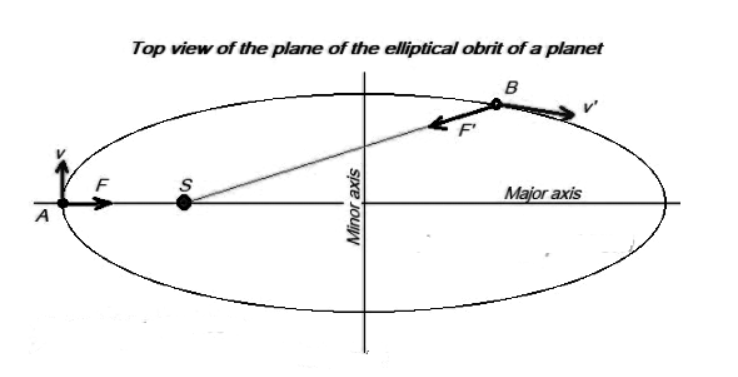
In this above figure we can see that
S- Sun at one of the focus
F,F’- gravitational pull on the planet A and B
v, v’- velocity of planet A and B
At A, \[F \bot v\]but at B, F’ is not \[ \bot \]v
 When the gravity is perpendicular to the direction of motion the work exhausted that part is zero. In an elliptical orbit, there are points, for example on the extremes of the foremost axis where this condition is fulfilled.
Hence (B) is true;
(D) isn't true.
At other points, the gravity isn't perpendicular to the motion, so work done won't be zero, so
(A) isn't true.
In one complete revolution, the displacement of the planet is zero, hence the work done is zero,
So (C) is true
Therefore option B and option C are taken into account because the right account subsequently.

Note - Anything that has mass also has gravity. Objects with more mass have more gravity. Gravity also gets weaker with distance. So, the closer objects are to every other, the stronger their gravitational pull is. Earth's gravity comes from all its mass. All its mass makes a combined gravitational pull on all the mass in your body.