Question

Consider a parallelogram, ABCD. AE is perpendicular to DC and CF is perpendicular to AD. If $AB = 16cm$, $AE = 8cm$ and $CF = 10cm$. Find AD.

Answer 1

Hint: First, we must need to know about the parallelogram.
Which is the quadrilateral with the two pairs of parallel sides in the geometry.
The facing sides and opposite sides of the parallelogram are the lengths in equal and opposite angles in the given parallelogram are equally measured.
It is more like the square in shape, but not exactly because in the square all the sides are equal but not in the parallelogram.
Formula used: Area of the parallelogram is $A = b \times h$, where b is the breadth and h is the height.

Complete step by step answer:
From the given information we construct a diagram of the parallelogram using AE is perpendicular to DC and CF is perpendicular to AD.

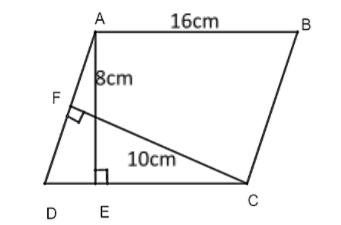
First, we need to find the area of the given parallelogram by the first side and then we will find the second side too.
After that, by comparing both of these sides we will find the value of AD.
Since from the information and diagram we see that $AE \bot DC,CF \bot AD$ and $AB = 16cm$, $AE = 8cm$and $CF = 10cm$
We need to find the value of AD,
So, $AB = DC = 16cm$(opposite sides of the given parallelogram are equal)
First find the area of the parallelogram, with the height AE and the base DC.
The area of the parallelogram ABCD is $ = b \times h$
The area of the parallelogram ABCD is $DC \times AE = 16 \times 8$
Thus, we get the area of the parallelogram as $128c{m^2}$
Now to find the area of the parallelogram for the CF as height and AD as the base.
Thus, we get the area of the parallelogram as $ABCD = CF \times AD \Rightarrow 128 = 10 \times AD$(as we already find the ABCD)
Further solving we get,
$ 128 = 10 \times AD \Rightarrow AD = 12.8cm$
Hence the value of the required AD is $12.8cm$

Note: While solving the parameters or parallelogram, there is a difference in the given height and base.
Different for the parallelogram but the pair of these will be fixed and the area will be the same for the parallelogram.
Since the area of the parallelogram is the breadth times multiplied by the given height.