Question

Consider a $\Delta ABC$ in the xy-plane with vertices A = (0,0), B = (1,1) and C = (9,1). If the line x = a divides the triangle into two parts of equal area, then a equals:
(a) 3
(b) 3.5
(c) 4
(d) 4.5

Answer 1

Hint: Start by drawing the diagrams. Once you draw the diagram, try to find the area of one-half of the two parts and equate it with half of the area of the old triangle.

Complete step-by-step answer:
Now let us start the above question by making the diagram.

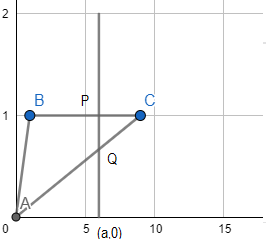
For triangle ABC, height is 1 unit, and the base BC is equal to 9-1 = 8 units. Therefore, the area of $\Delta ABC$ is equal to:
\[\Delta ABC=\dfrac{1}{2}\times b\times h=\dfrac{1}{2}\times 8\times 1=4\text{ uni}{{\text{t}}^{2}}\]
Now for the new triangle formed due to the line x=a is $\Delta PQC$ whose base PC is equal to 9-a. Now to find the height PQ, we need to find the point Q.
So, we let the equation of the line AC be $y=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)x$ . Which is:
$y=\dfrac{1}{9}x...........(i)$
Now, when x=a as in case of point q we get $y=\dfrac{1}{9}a$ . Therefore, point Q is $\left( a,\dfrac{1}{9}a \right)$ .
So, we can say that the height of $\Delta PQC$ is PQ which is equal to $1-\dfrac{1}{9}a$ . Therefore, the area of $\Delta PQC$ is:
\[ar\left( \Delta PQC \right)=\dfrac{1}{2}\times b\times h=\dfrac{1}{2}\times \left( 1-\dfrac{1}{9}a \right)\times \left( 9-a \right)uni{{t}^{2}}=\dfrac{{{\left( 9-a \right)}^{2}}}{18}\]
It is given in the question that $\Delta PQC$ should have half the area of $\Delta ABC$ . Using this, we get
$\dfrac{{{\left( 9-a \right)}^{2}}}{18}=\dfrac{1}{2}\times 4$
$\Rightarrow {{\left( 9-a \right)}^{2}}=36$
$\Rightarrow \left( 9-a \right)=6$
$\Rightarrow a=3$
Therefore, the answer to the above question is option (a).

Note: Remember that you could have used the condition of equal parts by equating the area of $\Delta PQC$ and the other quadrilateral that is formed but for this you need to find the area of the quadrilateral, which is a complex task, so, we avoided it in the above solution.