Question

How can complementary angles not be adjacent but share a common vertex?

Answer 1

Hint: To have complementary angles from a common vertex, the above scenario can be thought of as straight line over which a polygon with a right angle touches the straight line with its vertex, such that angles on either side of the polygon add up to give a total of \[{{90}^{\circ }}\]. This is based on the fact that a straight line measures \[{{180}^{\circ }}\]. Hence, we have complementary angles from a common vertex.

Complete step by step solution:
According to the given question, we are asked to think of a situation in which complementary angles are formed not from adjacent angles but rather they share a common vertex.
Complementary angle means when two angles add up to give a total of \[{{90}^{\circ }}\], they are said to complement.
There are many such scenarios which we can think of, such as the following.
Consider a straight line. We know that a straight line measures \[{{180}^{\circ }}\]. So, we have a straight line over which we place a polygon with an internal angle of \[{{90}^{\circ }}\] (like a right angled triangle, square, etc). Let us take a right angled triangle. We place this triangle over the line such that the vertex with the internal angle \[{{90}^{\circ }}\] touches the line.
We have the figure as follows:

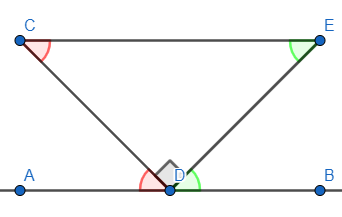
Here, AB is the straight line over which right angled triangle \[\vartriangle CDE\] is placed such that the vertex D with the internal angle \[\angle CDE={{90}^{\circ }}\]touches the line AB.
We can see in the figure that the line AB and side CE are parallel to each other. We know that in parallel lines, alternate angles are equal.
That is,
\[\angle ECD=\angle CDA\] and \[\angle CED=\angle EDB\]
We know that the internal angle sum of a right triangle is \[{{180}^{\circ }}\].
That is,
\[\angle ECD+\angle CED+\angle CDE={{180}^{\circ }}\]
We can see from the figure that \[\angle CDE={{90}^{\circ }}\], we get,
\[\Rightarrow \angle ECD+\angle CED+{{90}^{\circ }}={{180}^{\circ }}\]
\[\Rightarrow \angle ECD+\angle CED={{90}^{\circ }}\]
Since, we know that alternate angles in parallel lines are equal, we get,
\[\angle CDA+\angle EDB={{90}^{\circ }}\]
Therefore, \[\angle CDA\] and \[\angle EDB\] are complementary angles.

Note: We also know that a straight line measures \[{{180}^{\circ }}\]. We can prove through this fact as well.
The straight line we have is AB.
So, we have,
\[\angle CDA+\angle CDE+\angle EDB={{180}^{\circ }}\]
We know that \[\angle CDE={{90}^{\circ }}\] from the above figure,
\[\Rightarrow \angle CDA+{{90}^{\circ }}+\angle EDB={{180}^{\circ }}\]
Subtracting \[{{90}^{\circ }}\] from both the sides, we get,
\[\Rightarrow \angle CDA+{{90}^{\circ }}+\angle EDB-{{90}^{\circ }}={{180}^{\circ }}-{{90}^{\circ }}\]
\[\angle CDA+\angle EDB={{90}^{\circ }}\]
Therefore, \[\angle CDA\] and \[\angle EDB\] are complementary angles.