Question

Compare the areas under the curves $y={{\cos }^{2}}x\ and\ y={{\sin }^{2}}x$ between \[x=0\ and\ x=\pi \].

Answer 1

Hint: We will first start by drawing the rough sketch of the graph of both $y={{\cos }^{2}}x\ and\ y={{\sin }^{2}}x$. Then we will find the area between \[x=0\ and\ x=\pi \] and then compare the result.

Complete step-by-step answer:
Now, we will first draw the graph of $y={{\sin }^{2}}x\ and\ y={{\cos }^{2}}x$,

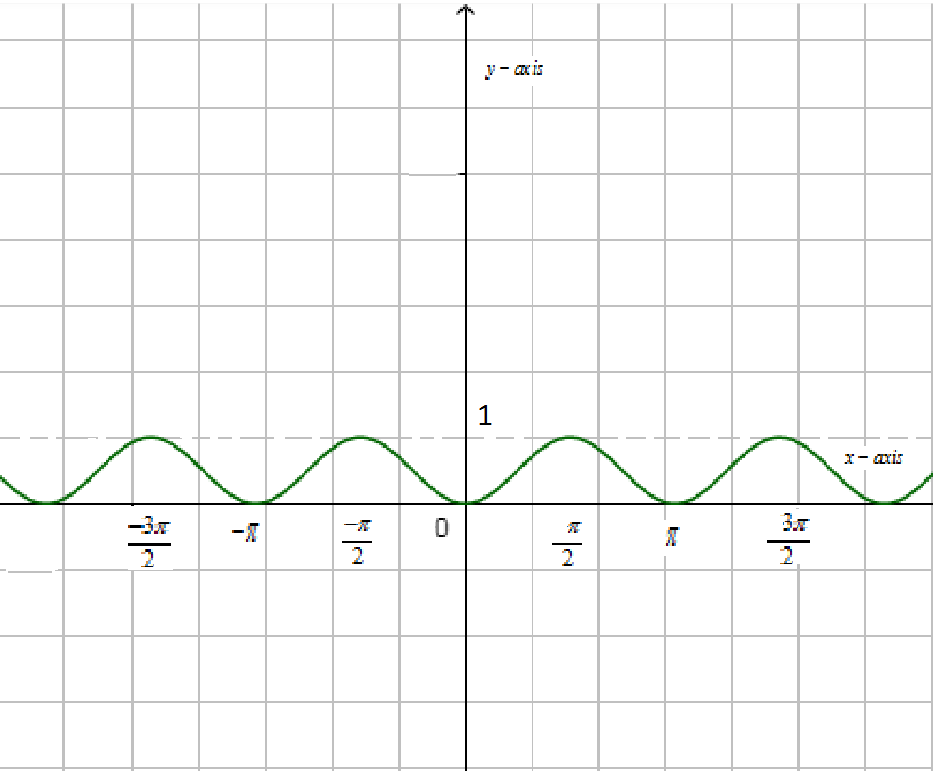
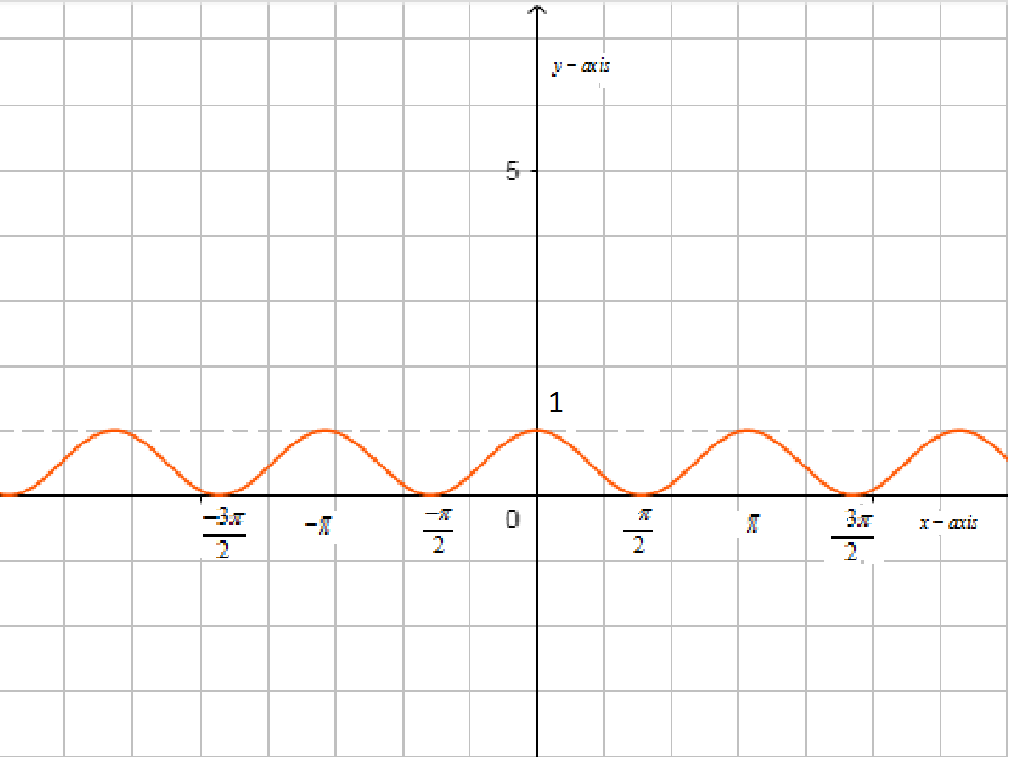
Now, we have to find the area of ${{\sin }^{2}}x$ between \[0\ to\ \pi \]. We know that the area under the curve is \[\int{f\left( x \right)dx}\].
\[\Rightarrow \int\limits_{0}^{\pi }{{{\sin }^{2}}xdx}\]
Now, we know the trigonometric identity that,
$\begin{align}
  & \cos 2x=1-2{{\sin }^{2}}x \\
 & \Rightarrow 1-\cos 2x=2{{\sin }^{2}}x \\
 & \Rightarrow {{\sin }^{2}}x=\dfrac{1-\cos 2x}{2} \\
\end{align}$
Now, using this in integral we have,
\[\begin{align}
  & \int\limits_{0}^{\pi }{\left( \dfrac{1-\cos 2x}{2} \right)} \\
 & \Rightarrow \int\limits_{0}^{\pi }{\left( \dfrac{1}{2}-\dfrac{1}{2}\cos 2x \right)}dx \\
\end{align}\]
Now, we know that,
\[\begin{align}
  & \int{\cos 2\theta =\dfrac{\sin 2\theta }{2}} \\
 & \Rightarrow \left( \dfrac{1}{2}x-\dfrac{1}{2}\dfrac{\sin 2x}{2} \right)_{0}^{\pi } \\
 & \Rightarrow \left. \dfrac{x}{2} \right|_{0}^{\pi }-\dfrac{1}{4}\left. \times \sin 2x \right|_{0}^{\pi } \\
 & \Rightarrow \dfrac{\pi }{2}-\dfrac{1}{4}\left( \sin 2\pi -\sin 0 \right) \\
 & \Rightarrow \dfrac{\pi }{2}-\dfrac{1}{4}\left( 0-0 \right) \\
 & \Rightarrow \dfrac{\pi }{2}sq\ units \\
\end{align}\]
Now, similarly for the area of \[{{\cos }^{2}}x\] we have,
\[\Rightarrow \int\limits_{0}^{\pi }{{{\cos }^{2}}xdx}\]
Now, we know that
\[\begin{align}
  & \cos 2x=2{{\cos }^{2}}x-1 \\
 & \dfrac{\cos 2x+1}{2}={{\cos }^{2}}x \\
\end{align}\]
So, using this we have,
\[\begin{align}
  & \int\limits_{0}^{\pi }{\left( \dfrac{\cos 2x+1}{2} \right)}dx \\
 & \Rightarrow \int\limits_{0}^{\pi }{\left( \dfrac{\cos 2x}{2}+\dfrac{1}{2} \right)}dx \\
 & \Rightarrow \left( \dfrac{\sin 2x}{4}+\dfrac{1}{2}x \right)_{0}^{\pi } \\
 & \Rightarrow \dfrac{\sin \left( 2\pi \right)-\sin \left( 0 \right)}{2}+\dfrac{1}{2}\left( \pi -0 \right) \\
 & \Rightarrow \dfrac{0-0}{4}+\dfrac{\pi }{2} \\
 & \Rightarrow \dfrac{\pi }{2}sq\ units \\
\end{align}\]
Now, we can see that the area of both \[{{\sin }^{2}}x\ and\ {{\cos }^{2}}x\] is \[\dfrac{\pi }{2}\] between \[0\ to\ \pi \]. Hence, their area is the same.

Note: It is important to note that we have used the trigonometric identity that $\cos 2x=1-2{{\cos }^{2}}x$ to solve the integral. Also, we have used the trigonometric identity that $\sin 2\pi =0$ and sin 0 = 0 to further solve it.