Question

 How many coins 1.75 cm in diameter and 2 mm thick must be melted to form a cuboid of dimensions \[11cm\times 10cm\times 7cm\] ?

Answer 1

Hint: We use the concept of “law of conservation of mass”, considering density to be constant and thus equating their volume before and after melting. First of all, let us suppose that “N” number of coins have to be melted to make the cuboid of the given dimension. So, we will have to calculate “N” i.e, the number of coins that have to be melted.

Complete step by step answer:
 In the above question, we will use the concept that the volume of the total coins must equal the volume of the cuboid formed after melting of coins. We are using the above concept considering there is no loss of material during melting as well as the density remains constant. Now, we will have to calculate the volume of total N coins and cuboid and make them equal.
Since, volume of cuboid \[=l\times b\times h\], where, l = length, b = width and h = height. Now, for the given cuboid, l = 11 cm, b = 10 cm and h = 7 cm.
So, the volume of the cuboid \[=\left( 11\times 10\times 7 \right)c{{m}^{3}}\Rightarrow 770c{{m}^{3}}\]
Now, we will have to calculate the volume of coins which is like a cylinder as shown below.

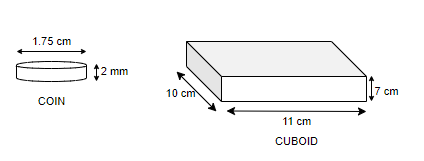
Since, the volume of the cylinder \[=\pi r^2h\] , where, r = radius and h = height. Now, for the given coin we have,
\[r=\dfrac{diameter}{2}\Rightarrow \dfrac{1.75}{2}\] cm and h = 2 mm = 0.2 cm.
So, the volume of the coin =\[\dfrac{\pi \times {{1.75}^{2}}\times 0.2}{4}\] \[c{{m}^{3}}\]
Therefore, the volume of “N” coins = \[c{{m}^{3}}\]
Now, we will equate the volume of the cuboid to the volume of “N” coins.
\[N\times \dfrac{\pi \times {{1.75}^{2}}\times 0.2}{4}=770\]
$\Rightarrow N=\dfrac{770\times 4}{\pi \times {{1.75}^{2}}\times 0.2}$
\[\Rightarrow\] N = 1601.45
So, the number of required coins will be 1601 (nearly).
Therefore, the answer of the above question will be equal to 1601.

Note: Take care of the unit while calculating where the thickness is given in “mm” and we have to change it in “cm” as all other units are in “cm”. The most common mistake that the student makes is by substituting diameter instead of radius in the formula to find the volume.