Question

Classify the given angle as acute, obtuse, straight, right, zero and complete angle.
$89.5^\circ $.

Answer 1

Hint: Here, we are required to classify the given angle under one of the given types of angles. We will first define all the angels mentioned in the definition. We will compare the given angle with the properties of the types of angles. The best possible match will help us to identify under which type, $89.5^\circ $ can be classified.

Complete step-by-step answer:
The meaning of the above mentioned six types of angles, i.e. acute, obtuse, straight, right, zero and complete angle is given below:
1.Acute Angle:
Acute angle is an angle which lies between $0^\circ $and $90^\circ $.
Hence, it cannot be equal to $90^\circ $i.e. it is always less than right angle.
Also, it cannot be equal to $0^\circ $ i.e. there will be always some distance between the two lines forming the angle.

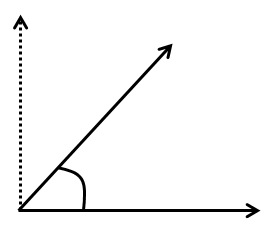
2.Obtuse Angle:
Obtuse angle is an angle which is greater than $90^\circ $ but less than$180^\circ $.
Hence, neither it is a straight line nor it forms a ‘L’ shape

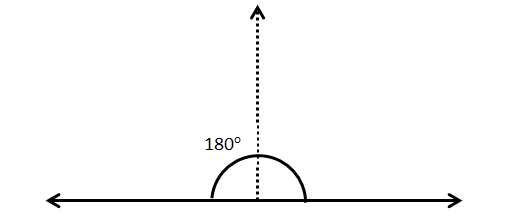
3.Straight Angle:
Straight angle is an angle which is equal to $180^\circ $, i.e.
It forms a straight line.

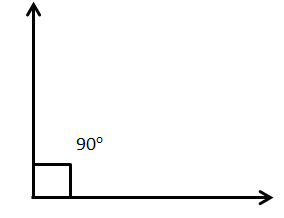
4.Right Angle:
Right angle is an angle which is equal to $90^\circ $, i.e. it forms an ‘L’ shape.
The two lines making a right angle are called perpendicular lines.

5.Zero Angle:
Zero angle is an angle which is equal to $0^\circ $.
This angle is formed when the two lines making an angle, lie on top of one-another.

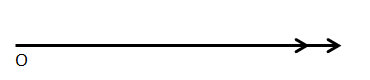
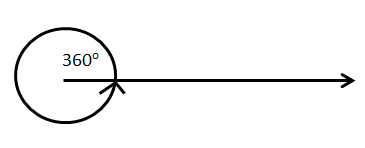
6.Complete Angle:
Complete angle is an angle which is full i.e. the measure of which is $360^\circ$

Now, with the help of above points, we can say that since, the angle $89.5^\circ $ is less than $90^\circ $
Therefore, clearly, it will form an acute angle.
Hence, the given angle is classified as an acute angle.
This is the required answer.
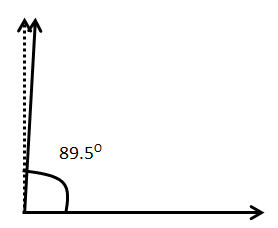
Note: We should know the different types of angles, their properties, and how they look. Since, $89.5^\circ $is an acute angle. Hence, it will look like:

We use degrees to measure angles but there is another term called ‘radians’ which is also used to measure the angles. Also, as we know one complete rotation or a full angle of a circle is $360^\circ $. Since the right angle is a quarter or one-fourth of a full circle. Therefore, its measure is $\dfrac{{360}}{4} = 90^\circ $. Hence, we always say that the right angle is equal to $90^\circ $.