Question

How many circles can be drawn through three noncollinear points
(a) only one
(b) two
(c) three
(d) infinite

Answer 1

Hint: To solve this question are should have knowledge of collinear points always lie in the same line while non-collinear never occurs all in the same line. Try drawing a circle or more using the given points and then check how many are possible.

We will first of all define certain terms to solve this question.
Collinear points – Three or more points are said to be collinear if they lie in the same straight line.
For example: In the figure below the points A, B and C are collinear.

Non – collinear point – Three or more points are called non – collinear points if they do not lie in the same straight line.
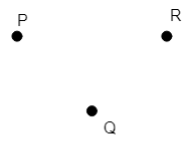
Example: In the figure below P, Q and R are non-collinear.
 

Here in this question, we are given three non-collinear points; let it be P, Q, and R. We will follow certain steps of construction to draw a circle using these points,

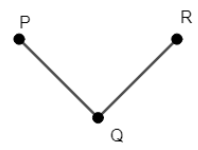
Step 1: Join PQ and QR.

Step 2: Using a compass draw perpendicular bisectors of line PQ and line QR. Name them as MN & ST respectively.

Le the point where they meet name as O.
Step 3: Taking O as the point on the compass and radius as OP draws a circle.

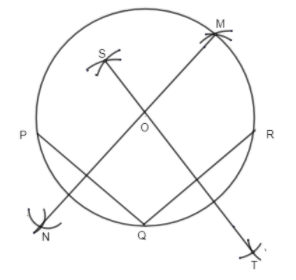
We have obtained only one circle using these three non-collinear points P, Q, and R.
Therefore only one circle can be obtained using three non-collinear points, which is an option (a).

Note: If the student has any possibility of confusion in the number of possible circles, then they can go for drawing more different perpendicular bisection the center O would anyway be the same. Hence the circle would also be the same. Therefore only one circle is possible.