
Choose the correct answer:
Statement 1
A common tangent to the circles \[{{x}^{2}}+{{y}^{2}}-6x=0\] and ${{x}^{2}}+{{y}^{2}}-10x+9=0$is given by $2y=x+3$
Statement 2
If two circles touch each other, their radical axis is the common tangent.
(a) Statement -1 is True, Statement 2 is True; Statement 2 is a correct explanation for Statement 1
(b) Statement 1 is True, Statement 2 is true; Statement 2 is NOT a correct explanation for Statement 1
(c) Statement 1 is True, Statement 2 is False
(d) Statement 1 is False, Statement 2 is True
Answer
602.7k+ views
Hint: First find out if the two circles intersect each other, touch each other or don’t touch or intersect each other at all. This would help you to determine the number of common tangents. Use the section formula that will give you the point of intersection of the common tangents. If the tangents are transverse common tangents, then the intersection point will divide them internally in the ratio of their radii, and if they’re direct common tangents, then they’d do the same externally.
The section formula for external division in the ratio m:n is $x=\dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},y=\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n}$.
For internal division, in the ratio m:n, it is $x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$
After finding the point like this, you can move on to finding the tangents passing through the point.
Complete step-by-step solution -
Let’s call the circle as $S_1$ \[{{x}^{2}}+{{y}^{2}}-6x=0\] and the circle ${{x}^{2}}+{{y}^{2}}-10x+9=0$ as $S_2$.
The general equation of any circle can be written as :
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$where the circle’s centre C=$(-g,-f)$and its radius $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
Therefore, for circle $S_1$, comparing the circle’s equation with the general form, we get :
$\begin{align}
& 2gx=-6x \\
& \Rightarrow g=-3 \\
\end{align}$
And, $\begin{align}
& 2fy=0 \\
& \Rightarrow f=0 \\
\end{align}$
Therefore, the centre of circle $S_1$, $C_1$ = $(-g,-f)=(3,0)$
And its radius ${{r}_{1}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ = $\sqrt{{{3}^{2}}+0-0}=\sqrt{9}=3$
For the circle $S_2$, we again compare its equation with the general form of circles, and see that :
\[\begin{align}
& 2gx=-10x \\
& \Rightarrow g=-5 \\
\end{align}\]
And, $\begin{align}
& 2fy=0 \\
& \Rightarrow f=0 \\
\end{align}$
Therefore, the centre of circle $S_2$, $C_2$ =$(-g,-f)$ =(5,0)
And its radius ${{r}_{2}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$= $\sqrt{{{5}^{2}}+0-9}=\sqrt{25-9}=4$
Before determining the common tangents, it is important to find out the number of common tangents these circles have.
We can do so by comparing the distances between the two centres and the sum of their radii.
If $({{r}_{1}}+{{r}_{2}})>|{{C}_{1}}-{{C}_{2}}|$this means that the circles intersect at more than one point.
($r_1$+$r_2$) = 7 and |$C_1$-$C_2$|= $\sqrt{{{(3-5)}^{2}}+{{(0-0)}^{2}}}=\sqrt{4}=2$
$\Rightarrow ({{r}_{1}}+{{r}_{2}})>|{{C}_{1}}-{{C}_{2}}|$
Since the circles intersect, the number of its common tangents will be 2 and both will be direct common tangents.
Next to make our calculations easier, we can find out where the two direct common tangents intersect.
We know that the point of intersection $(h,k)$ divides the line segment joining points $C_1$, $C_2$ and $(h,k)$ in the ratio of their radii externally.
That is, if we call the point $(h,k)$as D, then $\dfrac{{{C}_{2}}D}{{{C}_{1}}D}=\dfrac{{{r}_{2}}}{{{r}_{1}}}$
In the given question, the line joining $C_1$ and $C_2$ is $y=0$, since both the points lie on the $x$ axis.
Therefore, it is safe to assume that point D will be of the form (h,0) since it will also lie on the $x$ axis.
According to the rule that states, $\dfrac{{{C}_{1}}D}{{{C}_{2}}D}=\dfrac{{{r}_{1}}}{{{r}_{2}}}$
We can say that $\dfrac{\sqrt{{{(3-h)}^{2}}+{{(0-0)}^{2}}}}{\sqrt{{{(5-h)}^{2}}+{{(0-0)}^{2}}}}=\dfrac{3}{4}$
$\begin{align}
& \dfrac{3-h}{5-h}=\dfrac{3}{4} \\
& \Rightarrow 12-4h=15-3h \\
& \Rightarrow h=-3 \\
\end{align}$
Therefore, we now have the point of intersection of common tangents D as (-3,0).
We can now proceed with forming a general equation of the common tangents.
Since the common tangents will pass through the point (-3,0),
Their general equation can be written as :
$\dfrac{y-0}{x+3}=m$where m is the slope of the line, and is variable.
$\Rightarrow y=mx+3m$
$\Rightarrow mx-y+3m=0$ is the general equation of the line ………………………… (1)
Since the line we just found a general equation of is a tangent to both the circles, it means that the perpendicular distances of the centre of the circles from the line will be equal to their respective radii.
i.e. the perpendicular distance of $C_1$ from the line (1) = $r_1$
and perpendicular distance of $C_2$ from the line (1) = $r_2$
The perpendicular distance d of any point $(X,Y)$ from a line $Ax+By+C=0$ is given as:
$d=\dfrac{|AX+BY+C|}{\sqrt{{{m}^{2}}+1}}$
Like mentioned above, d for $C_1$ = $r_1$.
$\begin{align}
& {{r}_{1}}=\dfrac{|3m-0+3m|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow 3=\dfrac{|6m|}{\sqrt{{{m}^{2}}+1}} \\
\end{align}$
Squaring both sides, we get :
$\begin{align}
& 36{{m}^{2}}=9{{m}^{2}}+9 \\
& \Rightarrow 27{{m}^{2}}=9 \\
& \Rightarrow {{m}^{2}}=\dfrac{1}{3} \\
& \Rightarrow m=\pm \dfrac{1}{\sqrt{3}} \\
\end{align}$
Doing the same for the circle $S_2$, we’ll have :
$\begin{align}
& {{r}_{2}}=\dfrac{|5m-0+3m|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow 4=\dfrac{|8m|}{\sqrt{{{m}^{2}}+1}} \\
\end{align}$
Squaring both sides, we get :
$\begin{align}
& 64{{m}^{2}}=16{{m}^{2}}+16 \\
& \Rightarrow 48{{m}^{2}}=16 \\
& \Rightarrow {{m}^{2}}=\dfrac{1}{3} \\
& \Rightarrow m=\pm \dfrac{1}{\sqrt{3}} \\
\end{align}$
Since the values of m got by substituting for both the circles are the same, these values can be substituted in the general of the line that acts as common tangent for both the circles or the line (1).
The general equation of the line we found out was :
$mx-y+3m=0$
Substituting for m, we get two equations :
$\begin{align}
& \dfrac{x}{\sqrt{3}}-y+\dfrac{3}{\sqrt{3}}=0 \\
& \Rightarrow \sqrt{3}y=x+3 \\
\end{align}$
And
$\begin{align}
& -\dfrac{x}{\sqrt{3}}-y-\dfrac{3}{\sqrt{3}}=0 \\
& \Rightarrow \sqrt{3}y=-x-3 \\
\end{align}$
Both the equations mentioned above will act as common tangents for the two circles. Since the equation given in the question does not match either of the equations we’ve reached, we can thus conclude that Statement 1 is False.
As for concluding that Statement 2 is True, when the sum of the radii of two circles is equal to the distance between their centres, it means that both the circles touch each other at exactly one point, and in such cases they have three common tangents.
One of the common tangents is a transverse common tangent and since these two circles touch at exactly one point, the point where the tangent touches the two circles is the same as their own point of intersection.
This common tangent can be found by finding the radical axis of the two circles, provided they touch each other simply by finding the difference of the two circle equations.
Eq4 and eq3 depict the two tangents that we just found out.
Thus, Statement 2 is a True fact.
Hence, answer is (d) Statement 1 is False, Statement 2 is True.
Note: To ease your understanding here is a diagram of the two circles drawn to scale exactly
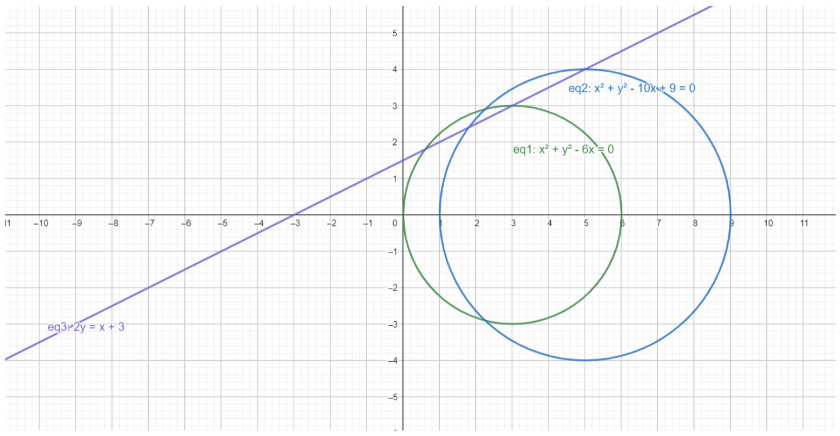
Here, eq3 shows the equation given in the question. Hence, we can see that this line doesn’t act as a tangent to any of the two circles.
The section formula for external division in the ratio m:n is $x=\dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},y=\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n}$.
For internal division, in the ratio m:n, it is $x=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},y=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}$
After finding the point like this, you can move on to finding the tangents passing through the point.
Complete step-by-step solution -
Let’s call the circle as $S_1$ \[{{x}^{2}}+{{y}^{2}}-6x=0\] and the circle ${{x}^{2}}+{{y}^{2}}-10x+9=0$ as $S_2$.
The general equation of any circle can be written as :
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$where the circle’s centre C=$(-g,-f)$and its radius $r=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$
Therefore, for circle $S_1$, comparing the circle’s equation with the general form, we get :
$\begin{align}
& 2gx=-6x \\
& \Rightarrow g=-3 \\
\end{align}$
And, $\begin{align}
& 2fy=0 \\
& \Rightarrow f=0 \\
\end{align}$
Therefore, the centre of circle $S_1$, $C_1$ = $(-g,-f)=(3,0)$
And its radius ${{r}_{1}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ = $\sqrt{{{3}^{2}}+0-0}=\sqrt{9}=3$
For the circle $S_2$, we again compare its equation with the general form of circles, and see that :
\[\begin{align}
& 2gx=-10x \\
& \Rightarrow g=-5 \\
\end{align}\]
And, $\begin{align}
& 2fy=0 \\
& \Rightarrow f=0 \\
\end{align}$
Therefore, the centre of circle $S_2$, $C_2$ =$(-g,-f)$ =(5,0)
And its radius ${{r}_{2}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}$= $\sqrt{{{5}^{2}}+0-9}=\sqrt{25-9}=4$
Before determining the common tangents, it is important to find out the number of common tangents these circles have.
We can do so by comparing the distances between the two centres and the sum of their radii.
If $({{r}_{1}}+{{r}_{2}})>|{{C}_{1}}-{{C}_{2}}|$this means that the circles intersect at more than one point.
($r_1$+$r_2$) = 7 and |$C_1$-$C_2$|= $\sqrt{{{(3-5)}^{2}}+{{(0-0)}^{2}}}=\sqrt{4}=2$
$\Rightarrow ({{r}_{1}}+{{r}_{2}})>|{{C}_{1}}-{{C}_{2}}|$
Since the circles intersect, the number of its common tangents will be 2 and both will be direct common tangents.
Next to make our calculations easier, we can find out where the two direct common tangents intersect.
We know that the point of intersection $(h,k)$ divides the line segment joining points $C_1$, $C_2$ and $(h,k)$ in the ratio of their radii externally.
That is, if we call the point $(h,k)$as D, then $\dfrac{{{C}_{2}}D}{{{C}_{1}}D}=\dfrac{{{r}_{2}}}{{{r}_{1}}}$
In the given question, the line joining $C_1$ and $C_2$ is $y=0$, since both the points lie on the $x$ axis.
Therefore, it is safe to assume that point D will be of the form (h,0) since it will also lie on the $x$ axis.
According to the rule that states, $\dfrac{{{C}_{1}}D}{{{C}_{2}}D}=\dfrac{{{r}_{1}}}{{{r}_{2}}}$
We can say that $\dfrac{\sqrt{{{(3-h)}^{2}}+{{(0-0)}^{2}}}}{\sqrt{{{(5-h)}^{2}}+{{(0-0)}^{2}}}}=\dfrac{3}{4}$
$\begin{align}
& \dfrac{3-h}{5-h}=\dfrac{3}{4} \\
& \Rightarrow 12-4h=15-3h \\
& \Rightarrow h=-3 \\
\end{align}$
Therefore, we now have the point of intersection of common tangents D as (-3,0).
We can now proceed with forming a general equation of the common tangents.
Since the common tangents will pass through the point (-3,0),
Their general equation can be written as :
$\dfrac{y-0}{x+3}=m$where m is the slope of the line, and is variable.
$\Rightarrow y=mx+3m$
$\Rightarrow mx-y+3m=0$ is the general equation of the line ………………………… (1)
Since the line we just found a general equation of is a tangent to both the circles, it means that the perpendicular distances of the centre of the circles from the line will be equal to their respective radii.
i.e. the perpendicular distance of $C_1$ from the line (1) = $r_1$
and perpendicular distance of $C_2$ from the line (1) = $r_2$
The perpendicular distance d of any point $(X,Y)$ from a line $Ax+By+C=0$ is given as:
$d=\dfrac{|AX+BY+C|}{\sqrt{{{m}^{2}}+1}}$
Like mentioned above, d for $C_1$ = $r_1$.
$\begin{align}
& {{r}_{1}}=\dfrac{|3m-0+3m|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow 3=\dfrac{|6m|}{\sqrt{{{m}^{2}}+1}} \\
\end{align}$
Squaring both sides, we get :
$\begin{align}
& 36{{m}^{2}}=9{{m}^{2}}+9 \\
& \Rightarrow 27{{m}^{2}}=9 \\
& \Rightarrow {{m}^{2}}=\dfrac{1}{3} \\
& \Rightarrow m=\pm \dfrac{1}{\sqrt{3}} \\
\end{align}$
Doing the same for the circle $S_2$, we’ll have :
$\begin{align}
& {{r}_{2}}=\dfrac{|5m-0+3m|}{\sqrt{{{m}^{2}}+1}} \\
& \Rightarrow 4=\dfrac{|8m|}{\sqrt{{{m}^{2}}+1}} \\
\end{align}$
Squaring both sides, we get :
$\begin{align}
& 64{{m}^{2}}=16{{m}^{2}}+16 \\
& \Rightarrow 48{{m}^{2}}=16 \\
& \Rightarrow {{m}^{2}}=\dfrac{1}{3} \\
& \Rightarrow m=\pm \dfrac{1}{\sqrt{3}} \\
\end{align}$
Since the values of m got by substituting for both the circles are the same, these values can be substituted in the general of the line that acts as common tangent for both the circles or the line (1).
The general equation of the line we found out was :
$mx-y+3m=0$
Substituting for m, we get two equations :
$\begin{align}
& \dfrac{x}{\sqrt{3}}-y+\dfrac{3}{\sqrt{3}}=0 \\
& \Rightarrow \sqrt{3}y=x+3 \\
\end{align}$
And
$\begin{align}
& -\dfrac{x}{\sqrt{3}}-y-\dfrac{3}{\sqrt{3}}=0 \\
& \Rightarrow \sqrt{3}y=-x-3 \\
\end{align}$
Both the equations mentioned above will act as common tangents for the two circles. Since the equation given in the question does not match either of the equations we’ve reached, we can thus conclude that Statement 1 is False.
As for concluding that Statement 2 is True, when the sum of the radii of two circles is equal to the distance between their centres, it means that both the circles touch each other at exactly one point, and in such cases they have three common tangents.
One of the common tangents is a transverse common tangent and since these two circles touch at exactly one point, the point where the tangent touches the two circles is the same as their own point of intersection.
This common tangent can be found by finding the radical axis of the two circles, provided they touch each other simply by finding the difference of the two circle equations.
Eq4 and eq3 depict the two tangents that we just found out.
Thus, Statement 2 is a True fact.
Hence, answer is (d) Statement 1 is False, Statement 2 is True.
Note: To ease your understanding here is a diagram of the two circles drawn to scale exactly

Here, eq3 shows the equation given in the question. Hence, we can see that this line doesn’t act as a tangent to any of the two circles.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




