Question

Check whether the pair of equations $5x-4y+8=0$ and $7x+6y-9$ is consistent or not.

Answer 1

Hint: First, we will write down the definition of linear equations and then we will write them down condition of linear equation in two variables being consistent that is $\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}$ then we will put the values from the given equations in this condition and get the answer.

Complete step by step answer:
The equations are given to us that is $5x-4y+8=0$ and $7x+6y-9$ are linear equations.
Let’s understand what are linear equations, linear equations are those equations that are of the first order. These equations are defined for lines in the coordinate system. A system of linear equations is just a set of two or more linear equations.
 A pair of linear equations in two variables, let’s say: ${{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}=0\text{ and }{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}=0$ , now, if equation has only one solution then $\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}$, the linear equations’ pair is called as consistent.

Now, we have with us: $5x-4y+8=0$ and $7x+6y-9$:
Where: ${{a}_{1}}=5,\text{ }{{b}_{1}}=-4,\text{ }{{c}_{1}}=8,\text{ }{{a}_{2}}=7,\text{ }{{b}_{2}}=6,\text{ }{{c}_{2}}=-9$
Now, $\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{5}{7}$ and $\dfrac{{{b}_{1}}}{{{b}_{2}}}=\dfrac{-4}{6}=\dfrac{-2}{3}$ , we see that $\dfrac{{{a}_{1}}}{{{a}_{2}}}\ne \dfrac{{{b}_{1}}}{{{b}_{2}}}$ , therefore it has a unique solution.

Hence, the given pair of linear equations is consistent.

Note:
 We can also solve this question by graphical method, that is first we will draw the graph of both lines that is: $5x-4y+8=0$ and $7x+6y-9$,

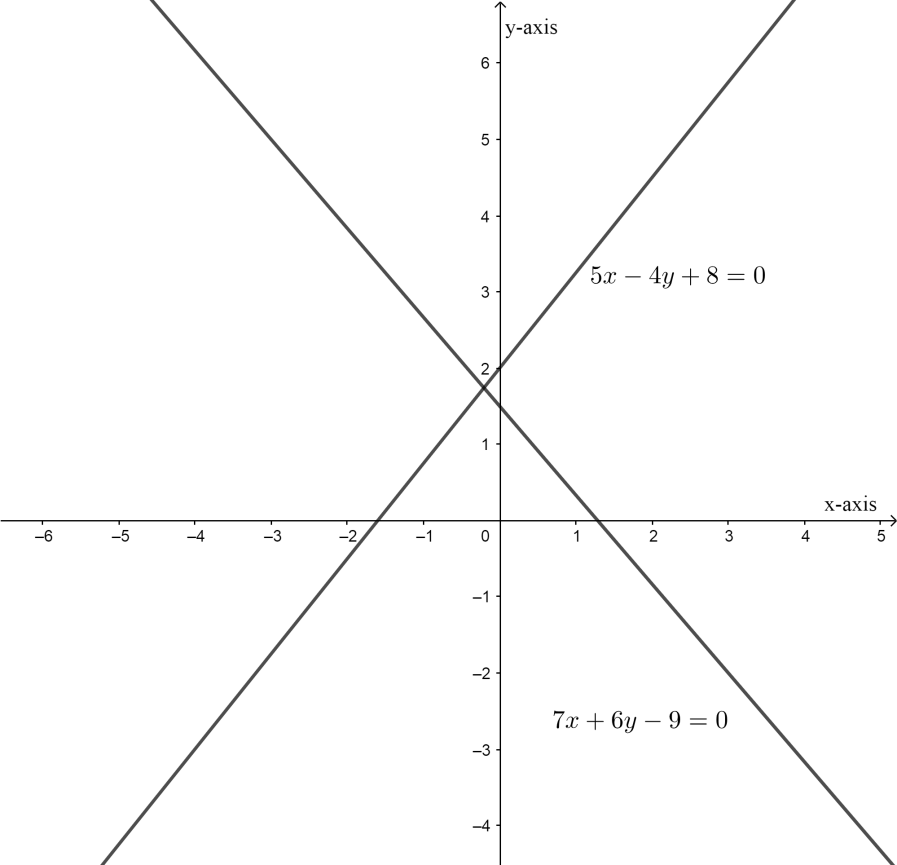
We see that they interact only at one point, therefore, they have a unique solution, and hence the system of linear equations given is consistent.
Remember that if two lines are coinciding then the pair of equations is said to be consistent as well as dependent.