Question

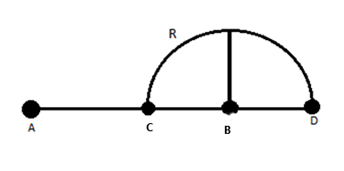
Charges $+q$ and $-q$ are placed at points A and B respectively which are a distance $2L$ apart, C is the midpoint between A and B. The work done in moving a charge $+Q$along the semicircle CRD is
A. $\dfrac{qQ}{2\pi {{\varepsilon }_{0}}L}$
B. $\dfrac{qQ}{6\pi {{\varepsilon }_{0}}L}$
C. $-\dfrac{qQ}{6\pi {{\varepsilon }_{0}}L}$
D. $\dfrac{qQ}{4\pi {{\varepsilon }_{0}}L}$

Answer 1

Hint: The work done by an electric force is proportional to the amount of the moved charge and proportional to the difference of potentials between the starting point and the destination.
${{W}_{(r)}}=Q\times {{V}_{(r)}}$
Potential at a distance ‘r’ from the center of a dipole is given by:
\[{{V}_{\left( r \right)}}=\dfrac{k2aq\cos \theta }{{{r}^{2}}-{{a}^{2}}{{\cos }^{2}}\theta }\]
Where;
             2a is distance between the two charges of the dipole
             q is the magnitude of charge of the dipole
$k=\dfrac{1}{4\pi {{\varepsilon }_{o}}}$

Complete answer:
It is given in the question that $'2L'$is the distance between the two charges of the dipole with point C as the center of the dipole.
Since the external charge $'+Q'$ undergoes a semicircular path from C to a point D with the center of the trajectory at point B. Hence, the radius of this semicircular path will be $'L'$.
Potential at the center of the dipole is $0$ .
This is because, at C:
${{V}_{C}}={{V}_{+q}}+{{V}_{-q}}$
\[{{V}_{C}}=\dfrac{kq}{L}+\dfrac{k(-q)}{L}\]
Therefore,
${{V}_{C}}=0$
Potential at point D due to the dipole is:
${{V}_{D}}=\dfrac{k(2Lq)\cos \theta }{{{(2L)}^{2}}-{{(L\cos \theta )}^{2}}}$
Since D lies on an axial position with respect to the dipole, $\theta ={{180}^{o}}$
Therefore $\cos \theta =-1$
$\Rightarrow $${{V}_{D}}=-\dfrac{k(2Lq)}{3{{(L)}^{2}}}$
$\because $$k=\dfrac{1}{4\pi {{\varepsilon }_{o}}}$
${{V}_{D}}=-\dfrac{(2q)}{4\pi {{\varepsilon }_{o}}(3L)}$
${{V}_{D}}=-\dfrac{(q)}{6\pi {{\varepsilon }_{o}}(L)}$
The work done to move $'+Q'$ from point C to D is:
${{W}_{CD}}=Q[{{V}_{D}}-{{V}_{c}}]$
${{W}_{CD}}=Q[-\dfrac{(q)}{6\pi {{\varepsilon }_{o}}(L)}-0]$
${{W}_{CD}}=-\dfrac{Q(q)}{6\pi {{\varepsilon }_{o}}(L)}$
Hence the correct option will be option C) $-\dfrac{Q(q)}{6\pi {{\varepsilon }_{o}}(L)}$

Note:
The work done to move charge $'+Q'$ from point C to point D is independent of the path undertaken and depends only on the initial and final positions of the charge.
Since the point D is closer to $-q$, the net potential at point D will be negative in magnitude.