Question

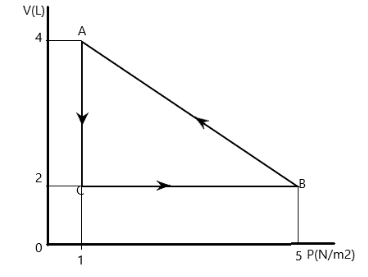
Calculate the work done for $ B \to A $

(A) $ 6 \times {10^{ - 3}}J $
(B) $ 12 \times {10^{ - 3}}J $
(C) $ 3 \times {10^{ - 3}}J $
(D) $ 4 \times {10^{ - 3}}J $

Answer 1

Hint: from B to A, observe that the pressure changes linearly. Generally work done can be defined as the integration of pressure with respect to volume through the path taken.

Formula used : In this solution we will be using the following formulae;
 $ W = \int {PdV} $ where $ W $ is the work done on a gas, $ P $ is the pressure of the gas and $ V $ is the volume of the gas.

Complete step by step answer:
To calculate the work done, we note that the pressure is linearly changing with volume, hence, we can model it as an equation of a straight line as in
 $ x = my + c $
Then, $ P = mV + c $
Now, from the diagram, we have that at volume equal to 2 litres (which is $ 2 \times {10^{ - 3}}{m^3} $ ), pressure is $ 5N/{m^2} $ .
Hence, $ 5 = m\left( {2 \times {{10}^{ - 3}}} \right) + c $
And similarly from diagram, we also get
 $ 1 = m\left( {4 \times {{10}^{ - 3}}} \right) + c $
Solving the two equations simultaneously, we get that
 $ m = - 2 \times {10^3} $ and $ c = 9 $
Hence, $ P = - 2 \times {10^3}V + 9 $
Now, the work done can be defined as
 $ W = \int {PdV} $ where $ W $ is the work done on a gas, $ P $ is the pressure of the gas and $ V $ is the volume of the gas.
So by inserting expression and integrating, we have
 $ W = \int_{{V_B}}^{{V_A}} {PdV} = \int_{2 \times {{10}^{ - 3}}}^{4 \times {{10}^{ - 3}}} {\left( { - 2 \times {{10}^3}V + 9} \right)dV} $
Hence, $ W = \left[ { - {{10}^3}{V^2} + 9V} \right]_{2 \times {{10}^{ - 3}}}^{4 \times {{10}^{ - 3}}} $
Hence, by carrying out the definite integral, we have that
 $ W = - 6 \times {10^{ - 3}}J $
We can neglect the negative sign as it only means that work is done by the gas from B to A, hence, we get
 $ W = 6 \times {10^{ - 3}}J $
Hence, the correct option is A.

Note:
For clarity, we can write the equation of a straight line as $ x = my + c $ . This is in contrast to the well known format of $ y = mx + c $ . However, it can be written the other way around too, which can be proven as in;
 $ y = mx + c $
 $ x = \dfrac{{y - c}}{m} = \dfrac{y}{m} - \dfrac{c}{m} $
But since $ m $ and c are constants, we have that $ \dfrac{1}{m} $ and $ \dfrac{c}{m} $ are constant. And there is the slope and intercept of the graph if $ x $ is considered the dependent variable. Hence
 $ x = {m_1}y - {c_1} $ .