Question

Calculate the wavelength from Balmer formula when n=3.

Answer 1

Hint: Try to use the Rydberg formula and derive the Balmer formula from there. There I have an equation that relates Rydberg constant, wavelength and the number of orbits the electron jumps into.


Complete step-by step answer:
In order to answer our question, we need to know about the line spectrum. The hydrogen spectrum is an example of line emission spectrum. The line spectrum of hydrogen is obtained by passing an electric discharge through hydrogen as at low pressure. Hydrogen molecules split up into atoms. These electrons absorb energy and electrons get discharged. When these excited electrons come back to ground state they emit electromagnetic radiation of discrete frequencies. Now, when these emitted radiations are passed through prism then discontinuous line spectrum of several isolated sharp lines is observed. This is how the line spectrum of hydrogen looks like:

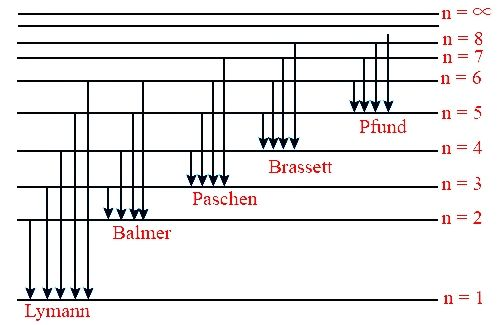
Now, the relation between wavelength and the number of spectral lines is: ${\displaystyle \frac{1}{\lambda }}=R{z}^2({\displaystyle \frac{1}{{n_1}^2}}-{\displaystyle \frac{1}{{n_2}^2}})$, where R= Rydbergs constant z=atomic number(1 in this case). When $n_1=2$, then the series of lines which are obtained by the above formula are called the Balmer series. The hydrogen spectrum consists of several series of spectral lines named after their discoverer. These series are Lyman series, Balmer series, Paschen series, Brackett series and Pfund series. The value $1.09\times {10}^7$ is called the Rydberg’s constant for the hydrogen atom. Now, let us find our answer by putting the values in the Balmer formula. So, we have:
${\displaystyle \frac{1}{\lambda }}=1.09\times {10}^7({\displaystyle \frac{1}{2^2}}-{\displaystyle \frac{1}{3^2}})=1.09\times {10}^7({\displaystyle \frac{1}{4}}-{\displaystyle \frac{1}{9}})=1.09\times {10}^7({\displaystyle \frac{5}{36}})$
So, we obtain
$\begin{array}{rl}& {\displaystyle \frac{1}{\lambda }}=1.52\times {10}^6\\ & So,\lambda =0.64\times {10}^{-6}m\end{array}$

So, the wavelength of the Balmer series for n=3 is $0.64\times {10}^{-6}m$.

NOTE: The following table shows the relation between the names of series, their ‘n’ values and their spectral region:

Series	$n_1$	$n_2$	Spectral Region
Lyman	1	2,3,..	Ultraviolet
Balmer	2	3,4,..	Visible
Paschen	3	4,5,…	Infrared
Brackett	4	5,6,…	Infrared
Pfund	5	6,7,….	Infrared