Question

Calculate the self-gravitational potential energy of matter forming (a) a thin uniform shell of mass M and radius R, and (b) a uniform sphere of mass m and radius R.

Answer 1

Hint: Gravitational self potential energy is the amount of work done to create an object of mass M formed by joining small masses of mass dm which were brought from infinity. Clearly, integration has to be performed by considering the potential created by for small mass m first.
Formula used:
Gravitational potential due to a mass m is:
$V = \dfrac{-Gm}{r}$

Complete answer:
(a) Consider a spherical shell of radius R. Let initially, a mass of m be equally distributed over this giving a potential of:
$V = \dfrac{-Gm}{R}$
on its surface.
We now bring a mass dm from infinity and add to this. Therefore, the work done in bringing the mass dm to a point on the surface of the sphere,
$dW = V dm = \dfrac{-Gmdm}{R}$
To find out the total work done in creating a mass of M, we integrate from 0 to M.
$U = \int_{0}^{M} \dfrac{-Gm}{R} dm = \dfrac{-G}{R} \left( \dfrac{m^2}{2} \right)_{0}^{M} = \dfrac{-GM^2}{2R}$

This is nothing but the gravitational self potential energy of the spherical shell of mass M and radius R.

(b) For the case of a solid sphere of radius R, there is a uniform mass distribution inside the sphere so it is not as simple as for the case of a shell. The density of the sphere has to be:
$d = \dfrac{M}{volume} = \dfrac{M}{(4/3) \pi R^3}$

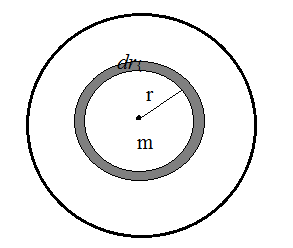
Now, in case of solid sphere, we perform mass additions in the form of shells of radius r, thickness dr so, we can write:
$dm = d \times 4 \pi r^2 dr$,
assuming the volume of the shell to be simply $4 \pi r^2 dr$.
Before adding this shell there was an initial mass m in the system constituting a sphere of radius r which is written as:
$m = d \times \dfrac{4}{3} \pi r^3$ .
Work done in addition of the shell to this mass m is:
$dW = V dm = \dfrac{-Gmdm}{r}$ .
Upon substituting for m and dm we get:
$dW = \dfrac{-16}{3} G \pi^2 d^2 r^4 dr$ .
Integrating on r from the limits 0 to R, we get:
$U = \dfrac{-16}{3} G \pi^2 d^2 \int_{0}^{R} r^4 dr$
$U = \dfrac{-16}{3} G \pi^2 d^2 \left( \dfrac{ r^5}{5} \right)_{0}^{R}$
Upon keeping the limits and substituting the value of d, we get the:
$U = \dfrac{-16}{3} G \pi^2 \left( \dfrac{M}{(4/3) \pi R^3} \right)^2 \left( \dfrac{ R^5}{5} \right) = \dfrac{-3GM^2}{5R}$ .

This is the required gravitational self potential energy for the case of a solid sphere.
So, for the case of (a) a thin uniform shell we have $\dfrac{-GM^2}{2R}$ and for the case of (b) a uniform sphere of mass m and radius R we have $\dfrac{-3GM^2}{5R}$.

Note:
Consider the case of electric potential, work done on a charge to bring it from infinity to a point in the vicinity of another charge with potential V is qV. Gravitational force is the force acting between masses therefore we wrote work to be Vdm. One can perform dimensional analysis if any confusion is present regarding this formula.