Question

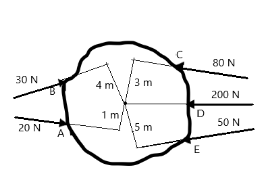
Calculate the resultant torque from the following diagram

Answer 1

Hint : The resultant force is the net torque produced by all the forces acting on the body. The torque in one direction should be positive and the other negative.

Formula used: In this solution we will be using the following formula;
 $ \Rightarrow {\vec T_{NET}} = \sum {\vec T} $ where, $ {\vec T_{NET}} $ is the net torque acting on a body, $ \vec T $ is the individual torque acting on the body.
 $ \Rightarrow T = FR $ , where $ T $ is the magnitude of the torque, $ F $ is the force acting on the body, and $ R $ is the perpendicular distance from the axis of interest.

Complete step by step answer
When there is a net torque on a body, it rotates about an axis with an angular acceleration, similarly to a net force creating a linear acceleration. Net torque can be given by
 $ \Rightarrow {\vec T_{NET}} = \sum {\vec T} $ where, $ {\vec T_{NET}} $ is the net torque acting on a body, $ \vec T $ is the individual torque acting on the body. Torque is a vector quantity, hence, torque in one direction must be made as positive and the other as negative.
Torque is given as
 $ \Rightarrow T = FR $ , where $ T $ is the magnitude of the torque, $ F $ is the force acting on the body, and $ R $ is the perpendicular distance from the axis of interest.
Now, making clockwise moment positive and anticlockwise moment negative, we have the torque about O to be
 $ \Rightarrow \vec T = (30 \times 4) - \left( {20 \times 1} \right) - \left( {80 \times 3} \right) + (200 \times 0) + \left( {50 \times 5} \right) $
By computation,
 $ \Rightarrow \vec T = 120 - 20 - 240 + 0 + 250 $
 $ \Rightarrow \vec T = 110Nm $ .
Hence, the net torque is 110 Nm in the clockwise direction.

Note
For clarity, distances were used directly because, as observed, the distance given already represents the perpendicular distance from the centre of rotation.
Also, we should observe that the 200 N, although a large force in itself, contributes nothing to the torque since its line of action passes through the centre axis. This attribute of torque is why many rotating equipment tend to have long handles, so forces applied to them may generate a large torque.