Question

How to calculate the largest area of a rectangle inscribed in a circle with a radius of 13?

Answer 1

Hint:
Given the radius of the circle. We have to calculate the largest area of the rectangle that can be inscribed in a circle. First, we will draw a rough diagram of a circle of radius 13 units and inscribe a rectangle inside it. Then, join the diagonal of the rectangle. Then, apply the Pythagoras theorem to the right angled triangle formed using diagonal as diameter of the circle. Then, apply the formula of the area of the rectangle to find the area. Then, find the maximum value of the trigonometric expression which is equal to the maximum area of the rectangle.

Complete step by step solution:
We are given the radius of the circle. First, we will draw a rough graph of the circle.

Now, we will draw the rectangle inscribed in it and join the diagonal of the rectangle.

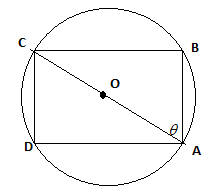
Now, we have ABCD rectangle inscribed in a circle of radius 13 units. Here, the semi circular angle with AC as a diameter of the circle forms a right angled triangle. Therefore,
\[ \Rightarrow AC = 2\left( {radius} \right)\]
\[ \Rightarrow AC = 2\left( {13} \right) = 26\]
Let the angle \[CAB = \theta \]
Now, determine the relation between the side AB and CA.
\[ \Rightarrow \dfrac{{AB}}{{CA}} = \cos \theta \]
\[ \Rightarrow AB = CA\cos \theta \] ……(1)
Also, determine the relation between the sides CB and CA.
\[ \Rightarrow \dfrac{{CB}}{{CA}} = \sin \theta \]
\[ \Rightarrow CB = CA\sin \theta \] ……(2)
Now, we will determine the area of the rectangle using the formula, \[A = l \times b\]
Here, \[l = CB\] and \[b = AB\]
\[ \Rightarrow A = CA\sin \theta \times CA\cos \theta \]
Simplify the expression, we get:
\[ \Rightarrow A = C{A^2}\sin \theta \cos \theta \]
Now, we will substitute \[AC = 26\].
\[ \Rightarrow A = {26^2}\sin \theta \cos \theta \]
Now, rewrite the expression to represent it as \[2\sin \theta \cos \theta \]
\[ \Rightarrow A = {13^2} \times 2 \times 2\sin \theta \cos \theta \]
Now, apply the trigonometric identity \[2\sin \theta \cos \theta = \sin 2\theta \] to the expression.
\[ \Rightarrow A = {13^2} \times 2\sin 2\theta \]
The area of the rectangle is maximum when \[\sin 2\theta \] will be maximum, that is \[\sin 2\theta \] must be equal to 1.
\[ \Rightarrow \sin 2\theta = 1\]
Write 1 as sine function.
\[ \Rightarrow \sin 2\theta = \sin 90^\circ \]
\[ \Rightarrow 2\theta = 90^\circ \]
\[ \Rightarrow \theta = 45^\circ \]
Now, compute the maximum area.
\[ \Rightarrow {A_{\max }} = {13^2} \times 2\]
\[ \Rightarrow {A_{\max }} = 338{\text{ sq}}{\text{. units}}\]

Final answer: Hence, the largest area of the rectangle at \[\theta = 45^\circ \] is \[338{\text{ sq}}{\text{. units}}\]

Note:
The students must remember that the perpendicular bisector of the circle divides the line segment into two equal parts. Here, in such types of questions, the diagonal BD bisects the line segment AC into two equal parts. Therefore, the length of diagonal AC is twice the radius of the circle OC or OA. The students must also remember that the value of \[\sin \theta \] must lie between zero and one, and \[\sin 90^\circ = 1\]