Question

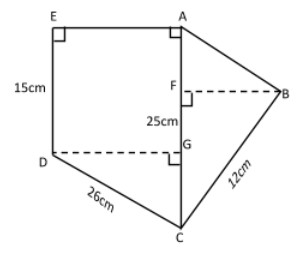
Calculate the area of the figure given below: which is not drawn to scale.
\[\begin{array}{*{20}{l}}
  {A.{\text{ }}630sq.cm} \\
  {B.{\text{ }}620sq.cm} \\
  {C.{\text{ }}640sq.cm} \\
  {D.{\text{ }}600sq.cm}
\end{array}\]

Answer 1

Hint: Joint DG divides DCAE into two polygons via ΔGCD and AGDE.
Further find area of $\Delta ABC$ and area of $\Delta GCD$ and the area of rectangle AGDE.
Then add the areas of two triangles$(\Delta ABC\,and\,\Delta GCD)$and rectangle AGDE.
Area of triangle $ = \dfrac{{base \times height}}{2}$ and area of rectangle\[ = length \times breadth.\]
Complete step by step solution:
From D, draw perpendicular such that\[DG \bot AC\] ,thereby,
making a right angled triangle GCD and rectangle AGDE.
Given: \[AC = 25cm\]
\[AC = AG + GC\]
As, \[AG = ED\] (opposite sides of rectangle)
\[\therefore AC = ED + GC\]
\[ \Rightarrow 25\,\,{\text{ = }}15 + GC\] \[\left[ {As{\text{ }}ED\; = 15{\text{ }}cm} \right]\]
⇒ GC = 25 -15 = 10 cm \[ \ldots .\left( 1 \right)\]
In \[\Delta GCD;\]
By using Pythagoras theorem,
${(hypotenuse)^2} = {(perpendicular\,)^2} + {(base)^2}$
\[C{D^2} = G{C^2} + G{D^2}\]
Or\[{26^2} = {10^2} + G{D^2}\] \[\left[ {GC = 10{\text{ }}cm{\text{ }}from{\text{ }}\left( 1 \right),CD = 26{\text{ }}cm{\text{ }}given} \right]\]
\[G{D^2} = {26^2} - {10^2}\]
\[ \Rightarrow 676-100 = 576\]
$GD = \sqrt {576} $
\[GD = 24{\text{ }}cm\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ldots .\left( 2 \right)\]
Entire figure consists of three parts viz;
\[\begin{array}{*{20}{l}}
  {\left( 1 \right)\Delta ABC} \\
  {\left( 2 \right)\Delta GCD} \\
  {\left( 3 \right)Rectangle{\text{ }}AGDE}
\end{array}\]
$\therefore ar(ABCDE) = ar(\Delta ABC) + ar(\Delta GCD) + ar(AGDE)$
\[ = \dfrac{1}{2} \times 25 \times 12 + \dfrac{1}{2} \times 10 \times 24 + 15 \times 24\] \[\left[ {GC = 10{\text{ }}cm{\text{ }}from{\text{ }}\left( 1 \right){\text{ }}and{\text{ }}GD = 24{\text{ }}cm{\text{ }}from{\text{ }}\left( 2 \right)} \right]\]
$ = 150 + 120 + 360$
$ = 630sq\,cm$
Thus, the area of the given figure is\[630sq{\text{ }}cm\] .
Hence, the correct option is A.
Note: In$\Delta ABC$and $\Delta GCD$one angle is \[90^\circ \]so, these two triangles are right angled triangles, that is why we used the formula area of triangle$ = \dfrac{1}{2} \times base \times height$.