Question

Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm, $\angle A = {90^ \circ }$ and
BC = CD = 52 cm.

Answer 1

Hint:
First, we will find the value of the BD.
Then by using the triangle formula, we will find $\Delta ABD$. Then after we will find the value of S.
To find the area of ABCD we have to find the value of ABD and ACD.

Complete step by step solution:

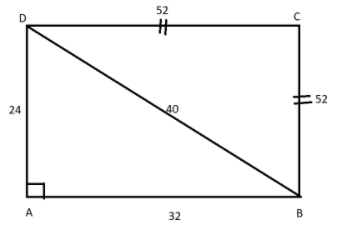
Here we have given the area of quadrilateral ABCD
AB = 32 cm (Given)
AD = 24 cm (Given)
 $\angle A = {90^ \circ }$ (Given)
BC = CD = 52 cm (Given)
Now,
${\left( {BD} \right)^2} = {\left( {AB} \right)^2} + {\left( {AD} \right)^2}$
$BD = \sqrt {{{\left( {32} \right)}^2} + {{\left( {24} \right)}^2}} $
$BD = 40cm$
By using triangle formula,
$\Rightarrow \Delta ABD = \dfrac{1}{2} \times AB \times AD$
$\Rightarrow \Delta ABD = \dfrac{1}{2} \times 32 \times 24$
$\Rightarrow \Delta ABD = 384c{m^2}$
For $\Delta BCD$ , a=52, b=52, c=40
S=$\dfrac{{a + b + c}}{2} = \dfrac{{52 + 52 + 40}}{2}$
$\Rightarrow S = \dfrac{{144}}{2} = 72cm$
By using formula, $\sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
$\Rightarrow ACD = \sqrt {72\left( {72 - 52} \right)\left( {72 - 52} \right)\left( {72 - 40} \right)} $
$\Rightarrow ACD = \sqrt {72 \times 20 \times 20 \times 32} $
$\Rightarrow ACD = \sqrt {36 \times 2 \times {{20}^2} \times 16 \times 2} $
$\Rightarrow ACD = 6 \times 4 \times 2 \times 20$
$\Rightarrow ACD = 960c{m^2}$
Now,
$\text{Area of ABCD} = ABD + ACD \\
\Rightarrow \text{Area of ABCD} = 384 + 960 \\
\Rightarrow \text{Area of ABCD} = 1344c{m^2}$

Note:
Quadrilateral: A quadrilateral is a polygon with four edges (sides) and four vertices (corner).
Other names for quadrilateral include “quadrangle” (in analogy to triangle), “tetragon” (in analogy to pentagon, 5-sided polygon, and hexagon, 6-sided polygon).
The word “quadrilateral” is derived from the Latin word “quadri”, a variant of four, and “latus”, meaning “side”.