Question

Bird S is flying at \[5{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] towards south, and bird T is flying at \[5\sqrt 2 {\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] towards the south-east. Then, velocity of bird S relative to bird T is:
A. \[10\sqrt 2 {\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] South-West
B. \[5{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] West
C. \[10\sqrt 2 {\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] North-West
D. \[5{\rm{ }}{{\rm{m}} {\left/
 {\vphantom {{\rm{m}} {\rm{s}}}} \right.
 } {\rm{s}}}\] East

Answer 1

Hint:The relative velocity of bird S relative to bird T is equal to the difference of their absolute velocities. We will draw the directions of bird S and bird T graphically, and we will find that the bird S is moving at an angle of \[45^\circ \] with east and south.

Complete step by step answer:
Let us first draw all the possible directions.

Here S represents the south, W represents the west, E represents east, and N represents north direction.
It is given that bird S is flying with \[5{\rm{ }}{{\rm{m}} {\left/
{\vphantom {{\rm{m}} {\rm{s}}}} \right.
} {\rm{s}}}\] towards the south, and bird T is flying with \[5\sqrt 2 {\rm{ }}{{\rm{m}} {\left/
{\vphantom {{\rm{m}} {\rm{s}}}} \right.
} {\rm{s}}}\] towards the south-east so we can represent it graphically, as shown below.

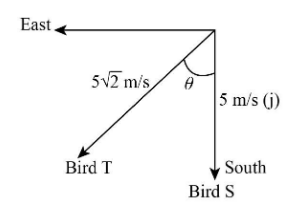
Let us consider positive j as north, negative j as south, positive i as east and negative i as west.
In vector form, we can write the velocity of the bird S as:
\[{V_s} = - 5\hat j\]
The velocity of bird T in vector form can be expressed as:
\[{V_T} = 5\sqrt 2 \sin \theta \hat i + 5\sqrt 2 \cos \theta \hat j\]
The direction of bird T is south-west, so we can substitute \[45^\circ \] for \[\theta \] in the above expression.
\[{V_T} = 5\sqrt 2 \sin 45^\circ \hat i + 5\sqrt 2 \cos 45^\circ \hat j\]
Taking direction into consideration, we can write:
\[{V_T} = - 5\hat i - 5\hat j\]
Let us write the expression for the relative velocity of bird S with respect to bird T.
\[{V_{ST}} = {V_S} - {V_T}\]
On substituting \[ - 5\hat j\] for \[{V_S}\] and \[ - 5\hat i - 5\hat j\] for \[{V_T}\] in the above expression, we get:
\[\begin{array}{l}
{V_{ST}} = - 5\hat j - \left( { - 5\hat i - 5\hat j} \right)\\
 = 5\hat i
\end{array}\]
We know that the positive i represents the east direction.
Therefore, bird S's relation velocity with respect to bird T is \[5{\rm{ }}{{\rm{m}} {\left/
{\vphantom {{\rm{m}} {\rm{s}}}} \right.
} {\rm{s}}}\] east, and option (B) is correct.

Note:Do not forget to consider the sign conventions while writing the velocity in vector form. Although we can decide the positive or negative direction as per our convenience, it is better to consider the downward direction as negative and upward as positive.