Question

How many balls, each of radius 1 cm, can be made from a solid sphere of lead of radius 8cm?
A) \[512\]
B) \[500\]
C) \[400\]
D) \[345\]

Answer 1

Hint: Here, as we can see this question conversion of one shape into another shape. So we apply the concept that the conversion volume remains the same. Therefore, to calculate the number of balls each of radius \[1{\text{ cm}}\] that can be made from a solid sphere of lead of radius \[8{\text{ cm}}\], first calculate the volume of the solid sphere of lead and the volume of ball that has to be made from the solid sphere of lead by applying the formula of volume of a solid sphere and then assume that \[x\] are the number of balls that can be made of solid sphere of lead, then the volume of the solid sphere of lead will be equal to \[x\] number of the balls multiply by the volume of the ball that has to made.

Complete step by step answer:
Given, the radius of the balls that must be made is \[1{\text{ cm}}\].
Volume of the balls that has to be made: \[V = \dfrac{4}{3}\pi {r^3}\]
Where, r is the radius of the sphere.
By applying volume of the sphere formula,
\[V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {\left( 1 \right)^3}\]

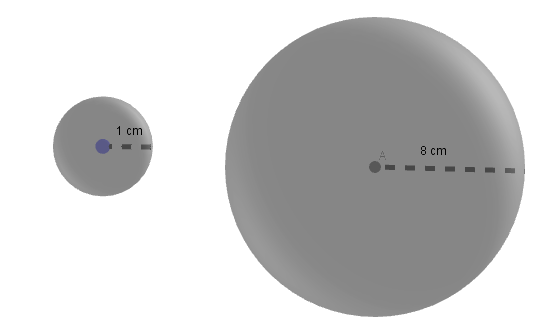
Given, radius of the solid sphere of lead is \[8{\text{ cm}}{\text{.}}\]
Volume of the solid sphere of lead is, \[V = \dfrac{4}{3}\pi {r^3}\]
By applying volume of the sphere formula,
\[V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {\left( 8 \right)^3}\]
Assume the number of balls with given radius \[1{\text{ cm}}\] that can be made out of the solid sphere of lead with given radius \[8{\text{ cm}}\] is \[ = x\].
So, the volume of the solid sphere of lead will be equal to the \[x\] number of the balls multiplied by the volume of the ball that has to be made.
\[
  \dfrac{4}{3}\pi {\left( 8 \right)^3} = x \times \dfrac{4}{3}\pi {\left( 1 \right)^3} \\
  {\left( 8 \right)^3} = x \\
  512 = x \\
 \]
Hence the number of balls with given radius 1cm that can be made out of the solid sphere of lead with given radius 8cm ] is \[512\].
So the correct option is A.

Note:
In these types of questions, always use the facts that in conversion of one same into another volume remains same. Always find the volumes of different shapes and equate them to get the result.