Question

At what angle the hands of a clock are inclined at 15minutes past 5?
A. \[{{58.5}^{\circ }}\]
B. \[{{64}^{\circ }}\]
C. \[{{67.5}^{\circ }}\]
D. \[{{72.5}^{\circ }}\]

Answer 1

Hint: We find \[{{\theta }_{H}}\]the angle hour hand makes when it moves from 12o’clock to 5:15 and \[{{\theta }_{M}}\]be the angle minute hand makes when it moves from 12o’clock to 5:15 Taking use of the fact that both the hour and minute hands create \[{{30}^{\circ }}\] when they change the time on the clock from one number to another The required angle in degrees for this problem is\[\theta ={{\theta }_{H}}-{{\theta }_{M}}\].

Complete step by step answer:
We all know that the 12 numerals from 1 to 12 on a watch signify time measurement. The hour hand is the shortest hand in the watch and it travels from one number to the next to signify one hour passing. The minute hand is the lengthier hand that depicts the passage of 5 minutes by moving from one number to the next.
When either the hour hand or minute hand move from 12 and then circle back to 12 they subtend a complete angle of measure\[{{360}^{\circ }}\]. So, the measure of angle when hour hand or minute hand when they move from one number to another is \[\dfrac{360}{12}={{30}^{\circ }}\]
 So an hour hand makes \[{{30}^{\circ }}\] in 1 hour and a minute hand makes \[{{30}^{\circ }}\]in every 5 minutes. We are asked to find the angle of inclination in between the hour and minute hand at 5:15. Consider\[{{\theta }_{H}}\]the angle hour hand makes when it moves from 12o’clock to 5:15 and \[{{\theta }_{M}}\]be the angle minute hand makes when it moves from 12o’clock to 3:40
 Therefore, \[\theta ={{\theta }_{H}}-{{\theta }_{M}}\]

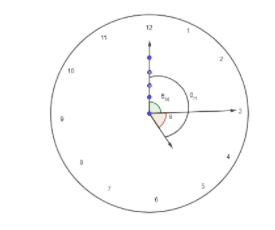
The hour hand advances from 12 to 5, passes 5 numbers, then points midway between 5 and 6 to indicate the positions for another 15 minutes. We already know that 60 minutes equals one hour.
So 15 minute is \[15\times \dfrac{1}{60}=\dfrac{1}{4}\]hours. So the hour hand has passed from12’o o'clock to 5:15 it passes\[5\dfrac{1}{4}=\dfrac{21}{4}\]hours. So we have
\[{{\theta }_{H}}=\dfrac{21}{4}\times {{30}^{\circ }}={{157.5}^{\circ }}\]
We see that the minute hand moves from 12 o'clock to 3 to show \[5\times 3=15\]minutes it passes 3 numbers we have,
\[{{\theta }_{M}}=3\times {{30}^{\circ }}={{90}^{\circ }}\]
So we have the angle of inclination is
\[\theta ={{\theta }_{H}}-{{\theta }_{M}}={{157.5}^{\circ }}-{{90}^{\circ }}={{67.5}^{\circ }}\]

So, the correct answer is “Option C”.

Note:
We see that we've frequently utilized the unitary technique with direct variation here, where we divide to discover the value of a single unit, then multiply to find the required value. We can directly find the required angle by the formula \[\Delta \theta =\left| {{\theta }_{h}}-{{\theta }_{m}} \right|\]where \[{{\theta }_{h}}={{0.5}^{\circ }}(60\times H\times M)\]and\[{{\theta }_{m}}={{6}^{\circ }}\times M\]where \[{{\theta }_{h}}\]and \[{{\theta }_{m}}\]are the angle of our hand and minute hand measured clockwise from 12o'clock positions, H is the hour and M is the minute passed hour.