Question

At the rate of Rs. 2 per sq m, cost of painting a rectangular floor is Rs 5760. If the length of the floor is 80% more than its breadth, then what is the length of the floor?

Answer 1

Complete step-by-step answer:
Hint: First find the area of the rectangular floor from the total cost and rate per square metre using the unitary method. Then use the relation between dimensions of the rectangular floor to calculate the length using the obtained area.

Complete step by step answer:
In the problem a rectangular floor is given.
The cost of painting this floor is Rs. 5760 at the rate of Rs. 2 per square meter.
Also, it is specified that the length of this rectangular floor is 80% more than its breadth.
We need to find the length of the floor.
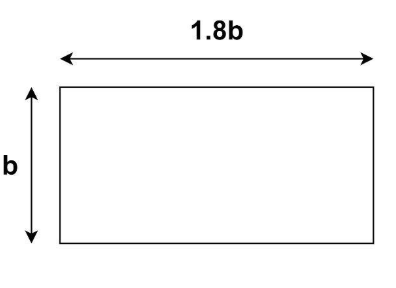
Let us assume that the breadth of the rectangular floor is $b$metres.
Then according to the problem, length of the floor is 80% more than its breadth,
$ \Rightarrow {\text{length}} = b + \dfrac{{80}}{{100}}b = b + 0.8b = 1.8b$metres.

Now we need to find the area of the rectangular floor in order to find its length.
In the problem it is given that the cost of painting the whole floor is Rs. 5760.
Also, the rate of painting one square meter of the floor is Rs. 2.
Using the unitary method to find the area of the rectangular floor.
Number of square meters painted in Rs. 2 $ = 1$square metre
Then the number of square meters painted in Re. 1 $ = \dfrac{1}{2}$square metre
Therefore, the number of square meters painted in Rs. 5760$ = \dfrac{1}{2} \times 5760 = 2880$square metres.
Hence the area of the rectangular floor is 2880 square metres.
Now according to the length and breadth assumed above, area of the rectangular floor is given by
$
  {\text{Area}} = {\text{length}} \times {\text{breadth}} \\
   \Rightarrow {\text{Area}} = \left( {1.8b} \right) \times b = 1.8{b^2} \\
$
Comparing it with the area of the rectangular floor, we get,
$
   \Rightarrow {\text{Area}} = 1.8{b^2} = 2880 \\
   \Rightarrow {b^2} = \dfrac{{2880}}{{1.8}} = 1600 \\
   \Rightarrow b = \sqrt {1600} = 40{\text{ metres}} \\
$
Therefore, length will be given by,
$ \Rightarrow {\text{length}} = 1.8b = 1.8 \times 40 = 72{\text{ metres}}$.
Hence the length of the rectangular floor is 72 metres.

Note: The unitary method is a technique for solving a problem by first finding the value of a single unit, and then finding the necessary value by multiplying the single unit value. In essence, this method is used to find the value of a unit from the value of a multiple, and hence the value of a multiple. One should try to form an equation in a single variable in problems like above. This should be done by transforming the other variables into the assumed one using the conditions given in the problem.