Question

At the foot of the mountain the elevation of its summit is \[{45^ \circ }\]; after ascending 1000 m towards the mountain up a slope of \[{30^ \circ }\] inclination, the elevation is found to be \[{60^ \circ }\]. The height of the mountain is
A. $\dfrac{{\sqrt 3 + 1}}{2}m$
B. $\dfrac{{\sqrt 3 - 1}}{2}m$
C. $\dfrac{{\sqrt 3 + 1}}{{2\sqrt 3 }}m$
D. None of these

Answer 1

Hint: We will first of all draw the diagram related to it. Now, we will use the trigonometric ratios of the known angles so that we can find the required lengths.

Complete step-by-step answer:
Let us draw the picture of it, taking AB as the height of the mountain.
So, we will get the following picture:-

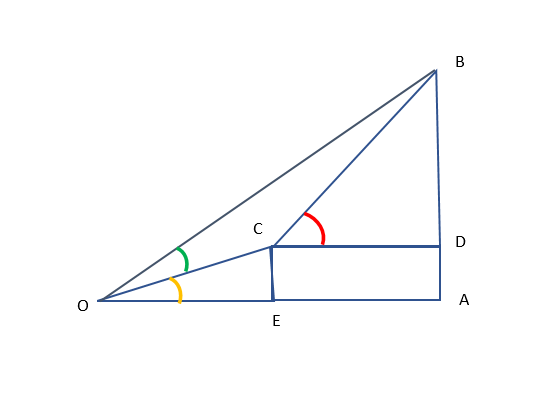
Since it is given that at the foot of the mountain the elevation of its summit is \[{45^ \circ }\], therefore, the sum of angle in yellow and green is \[{45^ \circ }\]and after ascending 1000 m towards the mountain up a slope of \[{30^ \circ }\] inclination, the elevation is found to be \[{60^ \circ }\], therefore, OC = 1000 m and the angle in yellow and red is \[{30^ \circ }\] and \[{60^ \circ }\] respectively.
Now, let us first go to triangle OCE:-
$ \Rightarrow \sin {30^ \circ } = \dfrac{{CE}}{{OC}}$
Since, OC = 1000 m and we know that $\sin {30^ \circ } = \dfrac{1}{2}$. Putting this in the above equation, we will get:-
$ \Rightarrow \dfrac{1}{2} = \dfrac{{CE}}{{1000}}$
Solving this above equation, we will then get:- CE = 500 m
$ \Rightarrow \cos {30^ \circ } = \dfrac{{OE}}{{OC}}$
Since, OC = 1000 m and we know that $\cos {30^ \circ } = \dfrac{{\sqrt 3 }}{2}$. Putting this in the above equation, we will get:-
$ \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{OE}}{{1000}}$
Solving this above equation, we will then get:- $OE = 500\sqrt 3 {\text{ }}m$
Now, let us now go to triangle AOB:-
$ \Rightarrow \tan {45^ \circ } = \dfrac{{AB}}{{OA}}$
We know that $\tan {45^ \circ } = 1$. Putting this in the above equation, we will get:-
$ \Rightarrow $AB = OA
Solving this above equation, we will then get:- CE = 500 m
$ \Rightarrow \cos {30^ \circ } = \dfrac{{OE}}{{OC}}$
If we take the height of the mountain AB = h meters.
$ \Rightarrow CD = EA = OA - OE = h - 500\sqrt 3 $ and BD = AB – AD = AB – CE = h – 500
Now, in triangle BCD:-
$ \Rightarrow \tan {60^ \circ } = \dfrac{{BD}}{{CD}}$
We know that $\tan {60^ \circ } = \sqrt 3 $. Putting this and $BD = h - 500$ and $CD = h - 500\sqrt 3 $ in the above equation, we will get:-
$ \Rightarrow \sqrt 3 = \dfrac{{h - 500}}{{h - 500\sqrt 3 }}$
Cross – multiplying both side to get:-
$ \Rightarrow \sqrt 3 h - 1500 = h - 500$
Taking h from right hand side to left hand side and the 1500 from left hand side to right hand side:-
$ \Rightarrow \sqrt 3 h - h = 1500 - 500$
Simplifying the above expression a bit to get:-
$ \Rightarrow \left( {\sqrt 3 - 1} \right)h = 1000$
Taking the constants from left hand side to right hand side, we will get:-
$ \Rightarrow h = \dfrac{{1000}}{{\sqrt 3 - 1}}m$ which is approximately 1.366 km.

Hence, the answer is 1.366 km.

Note:
The students must note that we used general trigonometric ratios whose value we already know to find the length of the sides we require.
In the last step we actually rationalized the denominator by multiplying and dividing the fraction by $\sqrt 3 + 1$ as follows:-
$ \Rightarrow h = \dfrac{{1000}}{{\sqrt 3 - 1}} \times \dfrac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}}$
Now, use the formula: ${a^2} - {b^2} = (a - b)(a + b)$ to get:-
$ \Rightarrow h = \dfrac{{1000\left( {\sqrt 3 + 1} \right)}}{{3 - 1}}$
$ \Rightarrow h = \dfrac{{1000\left( {\sqrt 3 + 1} \right)}}{2}$
$ \Rightarrow h = 500\left( {\sqrt 3 + 1} \right)$ meters
Hence, the correct option is (D).