Question

At a distance 2h from the foot of a tower of height h, the tower and a pole at the top of the tower subtend equal angles. Height of the pole should be
A.\[\dfrac{5H}{3}\ m\]
B.\[\dfrac{4H}{3}\ m\]
C.\[\dfrac{7H}{5}\ m\]
D.\[\dfrac{3H}{2}\ m\]

Answer 1

HINT:The formula for writing tangent of an angle is
\[\tan \theta =\dfrac{perpendicular}{base}\] .
We would also use the formula for tangent of twice the angle to evaluate the answer in this question as follows
\[\tan 2\alpha =\dfrac{\tan \alpha +\tan \alpha }{1-{{\tan }^{2}}\alpha }\]

Complete step by step answer:
As mentioned in the question, the figure would look like the below picture

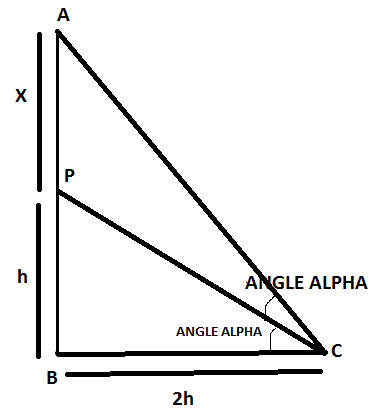
Now, on analyzing the figure above, we get to the equation as follows
 \[\begin{align}
  & In\ \Delta ABC, \\
 & \tan 2\alpha =\dfrac{\tan \alpha +\tan \alpha }{1-{{\tan }^{2}}\alpha } \\
\end{align}\]
Now, let the height of the pole be X. hence, we can write, using the formula mentioned in the hint, as follows
\[\begin{align}
  & In\ \Delta ABC, \\
 & \tan 2\alpha =\dfrac{X+H}{2H}\ \ \ \ \ ...(a) \\
\end{align}\]
Now, on similar grounds, we can write as
\[\begin{align}
  & In\ \Delta PBC, \\
 & \tan \alpha =\dfrac{H}{2H} \\
 & \tan \alpha =\dfrac{1}{2}\ \ \ \ \ ...(b) \\
\end{align}\]
Now, using the property mentioned in the hint, we can simplify equation (a) as follows
\[\tan 2\alpha =\dfrac{\tan \alpha +\tan \alpha }{1-{{\tan }^{2}}\alpha }=\dfrac{X+H}{2H}\]
On using the value from equation (b), we get
\[\begin{align}
  & \dfrac{\tan \alpha +\tan \alpha }{1-{{\tan }^{2}}\alpha }=\dfrac{X+H}{2H} \\
 & \dfrac{\dfrac{1}{2}+\dfrac{1}{2}}{1-\dfrac{1}{4}}=\dfrac{X+H}{2H} \\
 & \dfrac{1}{\dfrac{3}{4}}=\dfrac{X+H}{2H} \\
 & \dfrac{4}{3}=\dfrac{X+H}{2H}\ \ \ \ \ ...(c) \\
 & 3X+3H=8H \\
 & X=\dfrac{5H}{3}\ m \\
\end{align}\]
(On cross multiplying at step (c))
Hence, the height of the pole is \[\dfrac{5H}{3}\ m\] .

NOTE:The figure in this question is very tricky and is difficult to visualize it at first. Hence, the students can make an error while drawing the figure and then end up making a mistake and they would get to the correct solution.