Question

At 4:00 p.m. on a Sunday, a stick 2 feet tall casts a shadow 5 feet long. At the same time, a tree nearby casts a shadow 55 feet long. What is the height in feet of the tree?

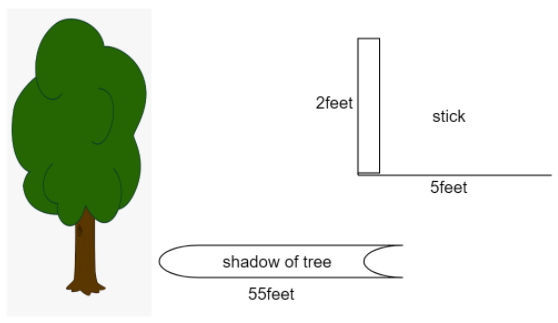
A.137.5
B.27.5
C.22
D.10

Answer 1

Hint: Here in this question the position of the sun will be fixed for both, that means angles subtended by the shadow on the top of the tree will also be the same. Use the trigonometric function for finding the height of the tree.

Complete step-by-step solution:

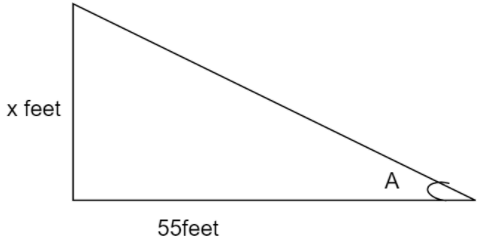
First let x be the height of the tree in feet and A in the diagram is theta.
As we have given height and base in the question so, we have to use the formula of $\tan \theta $
First, solve the function for stick
$\tan \theta = \dfrac{\text{height}}{\text{base}}$
Putting the values
$\tan \theta = \dfrac{2}{5}$
And now we have to find the value of $\tan \theta $ for the tree
$\tan \theta = \dfrac{\text{height}}{\text{base}}$
$\tan \theta = \dfrac{x}{{55}}$
As the position of the sun will be fixed for both, that means angles subtended by the shadow on the trip of the tree will also be the same
$\tan \theta {\text{ (for stick) = tan}}\theta {\text{ (for tree)}}$
$\dfrac{2}{5} = \dfrac{x}{{55}}$
Solve the equation and find the value of x
$x = \dfrac{{55 \times 2}}{5}$
Cancelling the denominator by numerator we get
$x = 22$
Hence the height in feet of the tree is 22 feet.

Note: Here students mostly get confused between the angle made by the tree and between the trigonometric function $\sin \theta ,\cos \theta $ and $\tan \theta $. Always let what you want to find. You must know the value of the trigonometric function $\tan \theta = \dfrac{\text{height}}{\text{base}}$. You have to assume that the position of the sun will be the same at the time.