Question

Assuming mass m of the charged particle, find the time period of oscillation.

$
  {\text{A}}{\text{. 2}}\pi \sqrt {\dfrac{{{q_1}q}}{{4\pi { \in _0}{a^3}m}}} \\
  {\text{B}}{\text{. 2}}\pi \sqrt {\dfrac{{4\pi { \in _0}{a^3}m}}{{{q_1}q}}} \\
  {\text{C}}{\text{. }}\dfrac{\pi }{2}\pi \sqrt {\dfrac{{{q_1}q}}{{4\pi { \in _0}{a^3}m}}} \\
  {\text{D}}{\text{. none of these}} \\
 $

Answer 1

Hint: The acceleration of a charge is equal to the product of square of angular frequency and the displacement. The force exerted on the charge is equal to the product of charge and the net electric field. By equating it with Newton’s second law, we can get acceleration and from acceleration we can get angular frequency and finally the time period.

Formula used:
Newton’s second law of motion:
$F = ma$
Force on a charge in electric field:
$F = qE$
Acceleration of an oscillating charge is given as
$a = {\omega ^2}x$
Time period is related to angular frequency by following relation:
$T = \dfrac{{2\pi }}{\omega }$
Here all the symbols have their usual meaning.

Complete answer:
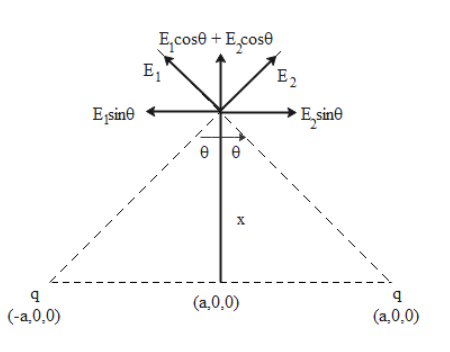
In the given diagram, we have two charges of the same magnitude at (-a,0,0) and (a,0,0). At a point along the line passing through the centre of the line joining the two charges, the various components of the electric field are shown. Since the charges have the same magnitude their electric fields also have the same values.
$|{E_1}| = |{E_2}| = E(let)$
Now the horizontal components of the electric field cancel each other while the vertical components get added up. Hence, the net electric field is given as
$E' = 2E\cos \theta = \dfrac{q}{{4\pi { \in _0}\left( {{x^2} + {a^2}} \right)}}\dfrac{x}{{\sqrt {{x^2} + {a^2}} }}$
The force due to this electric field on a charged particle ${q_1}$ of mass m is given as
$F = {q_1}E' = \dfrac{{{q_1}qx}}{{4\pi { \in _0}{{\left( {{x^2} + {a^2}} \right)}^{\dfrac{3}{2}}}}}$
If x << a then, $F = \dfrac{{{q_1}qx}}{{4\pi { \in _0}{a^3}}}$
Now using Newton’s second law, we get
$
  mA = \dfrac{{{q_1}qx}}{{4\pi { \in _0}{a^3}}} \\
  A = \dfrac{{{q_1}qx}}{{4\pi { \in _0}m{a^3}}} \\
 $
We denote acceleration by A.
As we know that acceleration of a charged particle undergoing oscillations is given as follows:
$\omega = \sqrt {\dfrac{A}{x}} = \sqrt {\dfrac{{{q_1}q}}{{4\pi { \in _0}m{a^3}}}} $
The time period is given as
$T = \dfrac{{2\pi }}{\omega } = 2\pi \sqrt {\dfrac{{4\pi { \in _0}m{a^3}}}{{{q_1}q}}} $

Hence, the correct answer is option B.

Note:
In this question the charge that is undergoing oscillation is a positive test charge. But in case, we had a negative charge then the directions of resultant forces would have been opposite to that for the positive charge. But the final answer would still remain the same in magnitude.