Question

Assuming 2s-2p mixing is not operative the paramagnetic species among the following is:
A) $\text{ B}{{\text{e}}_{\text{2 }}}$
B) $\text{ }{{\text{N}}_{\text{2 }}}$
C) $\text{ }{{\text{C}}_{\text{2 }}}$
D) $\text{ }{{\text{B}}_{\text{2 }}}$

Answer 1

Hint: The magnetic property of a molecule can be explained based on the molecular orbital theory. The molecule which does not contain the unpaired electron is known as the paramagnetic. The molecule which has all-electron paid-up does not contribute towards the magnetic property. It is diamagnetic in nature. To solve such a problem write down the MOT diagram of molecules.

Complete step by step solution:
The MOT diagram is drawn in such a way that we do not consider the s and p orbital mixing. Therefore the order of orbitals is not changed.
Let’s first draw the MOT of all molecules given in the problem.
A) $\text{ B}{{\text{e}}_{\text{2 }}}$ molecule: Beryllium atom has two electrons in the first shell and two-electrons in the second shell. The electronic configuration of the beryllium atom is as shown below,
$\text{ Be = 1}{{\text{s}}^{\text{2}}}\text{ 2}{{\text{s}}^{\text{2}}}\text{ }$
The $\text{ B}{{\text{e}}_{\text{2 }}}$molecule contains a total of 8 electrons in it. These 8 electrons are arranged in the molecular orbitals.
The MOT is as shown below,

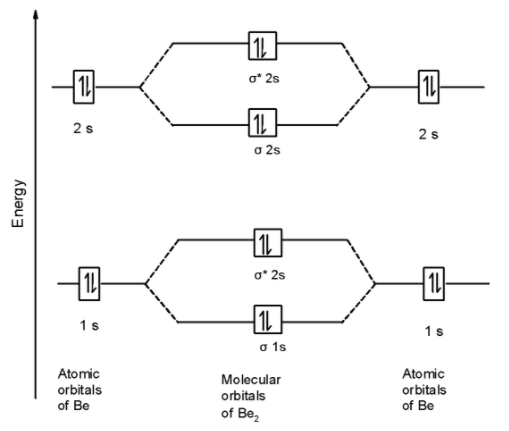
First of all, we can write the molecular orbital configuration of $\text{ B}{{\text{e}}_{\text{2}}}$ . The molecular orbital configuration of $\text{ B}{{\text{e}}_{\text{2}}}$ the molecule is as follows:
\[\]\[\text{ }\!\!\sigma\!\!\text{ 1}{{\text{s}}^{\text{2}}}\text{,}{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{1}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{ OR KK , }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{ }\]
Since, here all molecular orbitals contain the two electrons. These are all paired electrons. Thus $\text{ B}{{\text{e}}_{\text{2}}}$ the molecule is diamagnetic.
B) $\text{ }{{\text{N}}_{\text{2 }}}$ molecule : The nitrogen atom has three electrons in the 2p shell and 4 electrons in the innermost shell. The electronic configuration of nitrogen atom is as shown below,
$\text{ N = 1}{{\text{s}}^{\text{2}}}\text{ 2}{{\text{s}}^{\text{2}}}\text{ 2}{{\text{p}}^{\text{1}}}_{\text{x}}\text{= 2}{{\text{p}}^{\text{1}}}_{\text{y}}=\text{2}{{\text{p}}^{\text{1}}}_{z}\text{ }$
The $\text{ }{{\text{N}}_{\text{2 }}}$molecule contains a total of 14 electrons in it. These 14 electrons are arranged in the molecular orbitals. The MOT is as shown below,

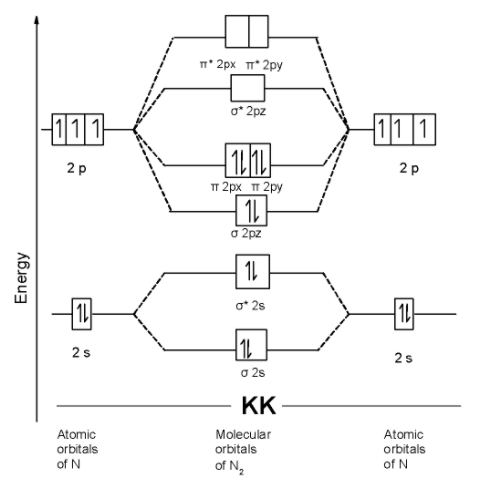
We can write the molecular orbital configuration of $\text{ }{{\text{N}}_{\text{2 }}}$ . The molecular orbital configuration of $\text{ B}{{\text{e}}_{\text{2}}}$ the molecule is as follows:
$\text{ }\!\!\sigma\!\!\text{ 1}{{\text{s}}^{\text{2}}}\text{,}{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{1}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{ , }\!\!\pi\!\!\text{ 2p}_{\text{y}}^{\text{2}}\text{ = }\!\!\pi\!\!\text{ 2p}_{\text{x}}^{\text{2}}\text{ , }\!\!\sigma\!\!\text{ 2p}_{\text{z}}^{\text{2}}\text{ }$
Since, here all molecular orbitals contain the two electrons. These are all paired electrons. Thus $\text{ }{{\text{N}}_{\text{2 }}}$ the molecule is diamagnetic.
C) $\text{ }{{\text{C}}_{\text{2 }}}$ Molecule: The carbon atom has two electrons in the 2p shell and 4 electrons in the innermost shell. The electronic configuration of nitrogen atom is as shown below,$\text{ C = 1}{{\text{s}}^{\text{2}}}\text{ 2}{{\text{s}}^{\text{2}}}\text{ 2}{{\text{p}}^{\text{1}}}_{\text{x}}\text{= 2}{{\text{p}}^{\text{1}}}_{\text{y}}=\text{2}{{\text{p}}^{0}}_{z}\text{ }$
The $\text{ }{{\text{C}}_{\text{2 }}}$molecule contains a total of 12 electrons in it. These 12 electrons are arranged in the molecular orbitals.
The MOT is as shown below,

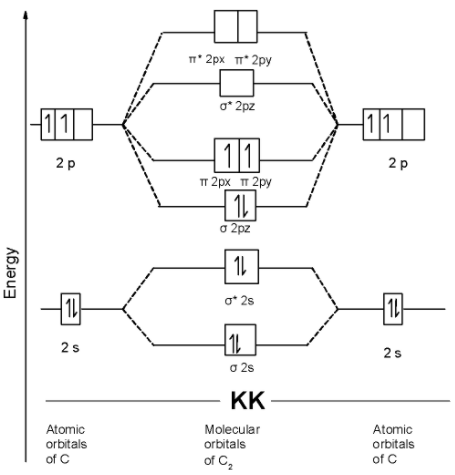
we can write the molecular orbital configuration of $\text{ }{{\text{C}}_{\text{2 }}}$ . The molecular orbital configuration of $\text{ }{{\text{C}}_{\text{2}}}$ the molecule is as follows:
$\text{ }\!\!\sigma\!\!\text{ 1}{{\text{s}}^{\text{2}}}\text{,}{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{1}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{ , }\!\!\sigma\!\!\text{ 2p}_{\text{z}}^{\text{2}},\text{ }\!\!\pi\!\!\text{ 2p}_{\text{y}}^{1}\text{ = }\!\!\pi\!\!\text{ 2p}_{\text{x}}^{1}\text{ }$
Since the pi molecular orbitals contain unpaired electrons. Thus $\text{ }{{\text{C}}_{\text{2 }}}$ the molecule is paramagnetic.
D) $\text{ }{{\text{B}}_{\text{2 }}}$molecule: The boron atom has one electron in the 2p shell and 4 electrons in the innermost shell. The electronic configuration of nitrogen atom is as shown below,
$\text{ B = 1}{{\text{s}}^{\text{2}}}\text{ 2}{{\text{s}}^{\text{2}}}\text{ 2}{{\text{p}}^{\text{1}}}_{\text{x}}\text{= 2}{{\text{p}}^{0}}_{\text{y}}=\text{2}{{\text{p}}^{0}}_{z}\text{ }$
The $\text{ }{{\text{B}}_{\text{2 }}}$molecule contains a total of 10 electrons in it. These 10 electrons are arranged in the molecular orbitals.
The MOT is as shown below,

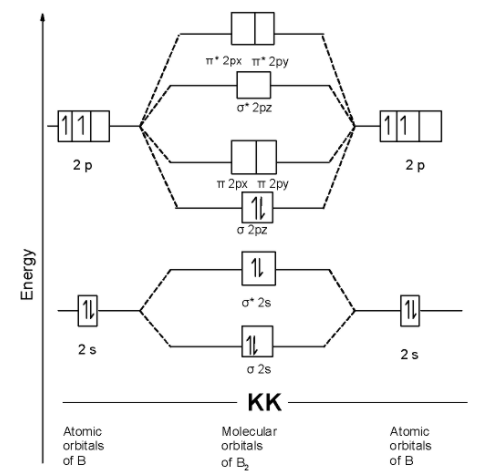
We can write the molecular orbital configuration of $\text{ }{{\text{B}}_{\text{2 }}}$ . The molecular orbital configuration of $\text{ }{{\text{B}}_{\text{2 }}}$ the molecule is as follows:$\text{ }\!\!\sigma\!\!\text{ 1}{{\text{s}}^{\text{2}}}\text{,}{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{1}{{\text{s}}^{\text{2}}}\text{, }\!\!\sigma\!\!\text{ 2}{{\text{s}}^{\text{2}}}\text{, }{{\text{ }\!\!\sigma\!\!\text{ }}^{\text{*}}}\text{2}{{\text{s}}^{\text{2}}}\text{ , }\!\!\sigma\!\!\text{ 2p}_{\text{z}}^{\text{2}}\text{ }$
Since the molecular orbitals theory does not contain the unpaired electron. Thus $\text{ }{{\text{B}}_{\text{2 }}}$ the molecule is diamagnetic.
Thus, from here we know that only $\text{ }{{\text{C}}_{\text{2 }}}$ molecule is paramagnetic.

Hence, (C) is the correct option.

Note: Note that, in atoms like $\text{ Li }$ , $\text{ Be }$ , $\text{ C }$ , $\text{ N }$ the energy difference is very small between the $\text{ 2s }$ and $\text{ 2p }$ orbitals. These are close to each other and thus p and s orbitals combine and lead to change in the expected order of the orbital energies. Here, we are not considering the mixing of s and p orbitals thus the carbon molecule is paramagnetic otherwise if we consider the mixing then the carbon molecule is diamagnetic.