Question

Assertion: Angle of repose is equal to the angle of limiting friction.
Reason: When the body is just at the point of motion, the force of friction in this stage is called limiting friction.
A) Both assertion and reason are correct and the reason is the correct explanation for the assertion.
B) Both assertion and reason are correct but reason is not the correct explanation for assertion.
C) Assertion is correct but reason is incorrect.
D) Both assertion and reason are incorrect.

Answer 1

Hint: Angle of friction is the angle made by the resultant of the normal reaction and limiting frictional force on the body with the normal reaction.
Angle of repose is the minimum angle of an inclined plane with the horizontal due to which a body starts to slide due to the effect of its own weight.
Using these definitions, try to find out the mathematical expression of the two angles as a function of their weight and try to check whether they are equal.

Complete step by step answer:
First let us consider the assertion.
The angle of limiting friction is the angle made by the resultant of the normal reaction and limiting frictional force on the body with the normal reaction.
Angle of repose is the minimum angle of an inclined plane with the horizontal due to which a body starts to slide due to the effect of its own weight.

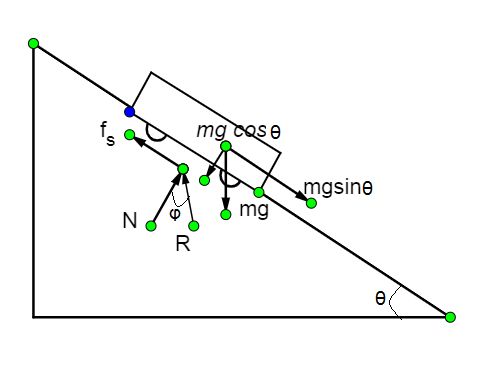
In the above figure, the cart is just about to move down the incline due to its own weight. Therefore, the angle of limiting friction is φ.
Also, the angle of repose is θ.

Now, in the state where the body is just about to move, limiting friction,
${{f}_{s}}={{\mu }_{s}}N$, --(1)
where μs is the coefficient of static friction.
Now, since the body is in a state of static equilibrium, we will equate forces in two axes, one along the incline and another one normal to the incline.
Equating forces normal to the incline,
$N=mg\cos \theta $ --(2)
Equating forces along the incline,
$mg\sin \theta ={{f}_{s}}$
$\therefore mg\sin \theta ={{\mu }_{s}}N$ -from (1)
$\therefore mg\sin \theta ={{\mu }_{s}}mg\cos \theta $ -- from (2)
$\therefore \tan \theta ={{\mu }_{s}}$ --(3)
Now, for the frictional and normal forces, according to the diagram,
$\tan \phi =\dfrac{{{f}_{s}}}{N}=\dfrac{{{\mu }_{s}}N}{N}={{\mu }_{s}}$ --(4)
From (3) and (4) we see that $\tan \theta =\tan \phi $
$\therefore \theta =\phi $
Or, $\text{Angle of repose = Angle of limiting friction }$
Hence the assertion is correct.
When the body is just about to be in motion, the frictional force on the body is called the limiting friction. This is true, but does not seem to be the proper explanation for the reason.
Hence, the assertion and reason both are correct but the reason is not the correct explanation for the assertion.
Hence (B) is correct.

Note: A proper explanation for the assertion would be that since at limiting friction, the angle of the incline becomes the angle of repose, so the assertion is correct.
Actually the angle of the incline is always equal to the angle of friction for static equilibrium. It is only at the limiting friction case that the angle of the incline becomes the angle of repose.