Question

As observed from the top of a 150m tall lighthouse, the angles of depression of two ships approaching it are ${30^0}{\text{ and }}{45^0}$. If one ship is directly behind the other, find the distance between the two ships.

Answer 1

Hint: Using the property of alternate angles $\angle EAD = \angle ADC$ and $\angle EAC = \angle ACB$. Thus eventually using the angle of depression we have arrived at a certain angle of elevation from the point C and D for ship 1 and ship 2 respectively.

Complete Step-by-Step solution:

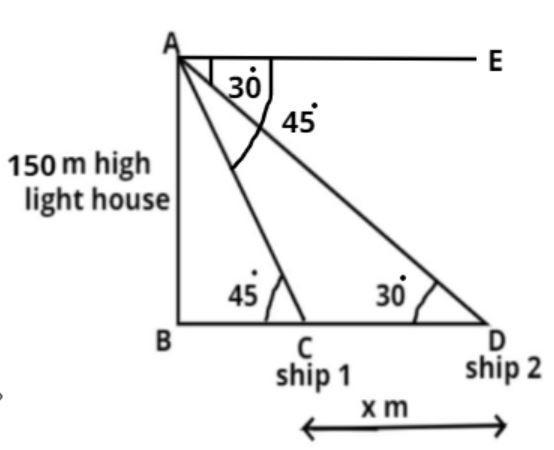
Let AB be the light house. The height (h) of the lighthouse from the sea level is AB = h = 150 m.
Now the angle of depression of the ships is 30 degree and 45 degree and the one ship is exactly behind the other one on the same side of the light house (see figure).
Now we have to find out the distance between the ships.
Let the distance be x m (see figure).
$ \Rightarrow CD = x$ meter.
In triangle ABC,
$\tan {45^0} = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \dfrac{{AB}}{{BC}} = \dfrac{{150}}{{BC}}$
As we know $\tan {45^0} = 1$
$ \Rightarrow BC = 150$ meter.
Now in triangle ABD
$\tan {30^0} = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \dfrac{{AB}}{{BD}}$
As we know $\tan {30^0} = \dfrac{1}{{\sqrt 3 }}$
So substitute this value in above equation we have,
$ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{150}}{{BD}}$
$ \Rightarrow BD = 150\sqrt 3 $ meter.
So from figure CD = BD – BC
So, substitute the values of BD and BC in above equation we have
$\therefore CD = 150\sqrt 3 - 150$
$ \Rightarrow x = 150\left( {\sqrt 3 - 1} \right)$ meter.
Now simplifying this we have,
$ \Rightarrow x = 150\left( {1.732 - 1} \right) = 150\left( {0.732} \right) = 109.8$ meter. $\left[ {\because \sqrt 3 = 1.732} \right]$
So, the distance between two ships is 109.8 meter.
So, this is the required answer.

Note: Whenever we face such type of height and distance problems the key concept is to have a diagrammatic representation of the information provided in the question as it helps in understanding the basic geometry of the figure. Use the concept of basic trigonometric ratios in respective triangles to get the answer.