Question

As observed from the top of a \[100\]m high lighthouse from the sea-level, the angles of depression of two ships are \[30{}^\circ \]and \[45{}^\circ \]. If one ship is exactly behind the other on the same side of the light house, find the distance between the two ships. [Use\[\sqrt{3}=1\cdot 732\]]

Answer 1

Hint: In this question we need to draw the first diagram carefully. Then we use the basic property of trigonometric ratio in terms of right angle triangle side.
In general if we consider triangle ABC as below

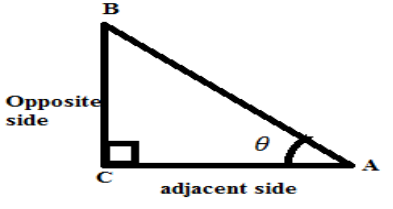
\[\text{tan }\!\!\theta\!\!\text{ =}\dfrac{\text{opposite side}}{\text{adjacent side}}\]

Complete step-by-step solution -
Now: Let’s start drawing a diagram based on the given question (by reading each line).

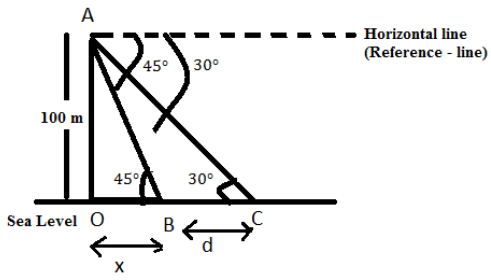
From figure OA is the height of the lighthouse , ship $1$ is at point C and ship $2$ is at point B.
As we know that; angle of depression is the angle between the horizontal line (Reference line) and the line of sight of the object from the reference line.
Now, Let the distance of ship $2$ from the light house be [i.e. OB = x] and let the distance between two ships be [i.e. BC=d]
Now, we have to find
Using Trigonometric Ratio Table;
\[\text{tan }\!\!\theta\!\!\text{ =}\dfrac{\text{opposite side}}{\text{adjacent side}}\]
Now, In right angled Triangle OAB, OA is on the opposite side and OB is on the adjacent side. Hence we can write
\[\Rightarrow \tan 45{}^\circ =\dfrac{OA}{OB}\] \[\text{ }\!\!\{\!\!\text{ }\because \text{tan45 }\!\!{}^\circ\!\!\text{ = 1 }\!\!\}\!\!\text{ }\]
\[\Rightarrow 1\text{=}\dfrac{\text{100 m}}{\text{x}}\]
\[\Rightarrow x\text{=100 m}\] ………………………….. (i)
In the right angled Triangle OAC; OA is on the opposite side and OC is adjacent side. Hence we can write
\[\Rightarrow \text{tan30 }\!\!{}^\circ\!\!\text{ =}\dfrac{\text{OA}}{\text{OC}}\]
\[\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{100}{x+d}\]
\[\Rightarrow x+d=100\sqrt{3}\]
From equation (i) we can substitute value of x:
\[\Rightarrow 100+d=100\sqrt{3}\]
\[\Rightarrow d=100\sqrt{3}-100\]
\[\Rightarrow d=100[\sqrt{3}-1]\]
\[\Rightarrow d=100[1\cdot 732-1]\] [\[\because \]given \[\sqrt{3}=1\cdot 732\]]
\[\Rightarrow d=100\times 0\cdot 732\]
\[\Rightarrow d=\text{73}\text{.2 m}\]
Therefore, the distance between two ships is \[''73\cdot 2\,m''\].

Note: In this type of question we have to be careful about allocation of objects in the form of a triangle is very important. Smaller angle is always far away as compared to a greater angle. Here we can also use the similarity property of triangles between triangle AOB and AOC and find the relation between the sides.