Question

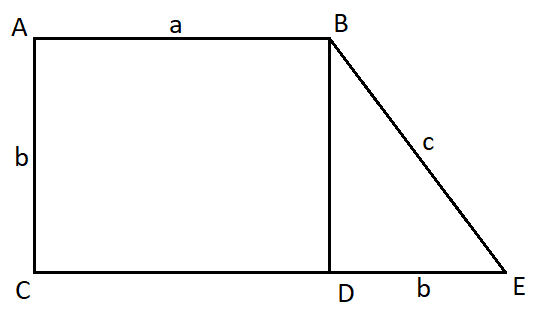
What is the area of the given figure? ABCD is a rectangle and BDE is an isosceles right triangle.

(A) $ab$
(B) $a{b^2}$
(C) $cab$
(D) $b\left( {a + \dfrac{b}{2}} \right)$

Answer 1

Hint: The figure given in the problem is the combination of two shapes, a rectangle ABCD and an isosceles triangle BDE. So the area of the given figure will be the addition of the areas of these two parts. The area of the rectangle is length time width. And the area of a triangle is half times the product of perpendicular and base. Use this to form an equation and substitute the values given in the figure.

Complete step-by-step answer:
Here in this problem, we are given the figure, which consists of a rectangle ABCD and an isosceles triangle BDE. They both share a common side BD. The length and width of the rectangle are given as ‘a’ and ‘b’ respectively. The length of the base DE of the triangle is given as ‘b’ and the length of the hypotenuse is ‘c’. With this given information we need to find the correct expression for the area of the figure from the four given options.

From the figure, it is clear that the figure is the combination of two parts, one is a rectangle ABCD and the other is an isosceles right angle triangle BDE, sharing a common side BD.
The total area of the figure ABEDC can be given by the area of rectangle ABCD and the triangle BDE
$ \Rightarrow Area{\text{ }}ABEDC = Area{\text{ }}ABCD + Area{\text{ }}BDE$
As we know that the area of the rectangle is calculated by multiplying its length and breadth. And the area of the triangle is given by half of the product of base and perpendicular. So the above equation will become:
 $ \Rightarrow Area{\text{ }}ABEDC = Area{\text{ }}ABCD + Area{\text{ }}BDE = \left( {AB \times AC} \right) + \left( {\dfrac{1}{2} \times DE \times BD} \right)$
Now we can substitute the known values in the above equation. We already know the values$AB = a,AC = b,DE = b{\text{ and }}BD = DE = b$ (since the perpendicular and base of an isosceles right and triangle are equal). We can put these values into the above equation:
$ \Rightarrow Area{\text{ }}ABEDC = \left( {AB \times AC} \right) + \left( {\dfrac{1}{2} \times DE \times BD} \right) = \left( {a \times b} \right) + \left( {\dfrac{1}{2} \times b \times b} \right)$
Therefore, we get the area of the figure as $\left( {ab + \dfrac{{{b^2}}}{2}} \right){\text{ uni}}{{\text{t}}^2}$ .
The area can also be written as $b\left( {a + \dfrac{b}{2}} \right){\text{ uni}}{{\text{t}}^2}$ to match the given options.
Hence, the option (D) is the correct answer.

Note: In mensuration, solving the problems gets easier when we know the correct formula to be used. Be careful while substituting the values in the equation. A rectangle is a four-sided two-dimensional shape that consists of four right-angle vertices and two pairs of equal sides. And an isosceles right-angled triangle is a three-sided shape with two equal sides having a right angle between them.