Question

What is the area of the equilateral triangle whose side length is a?

Answer 1

Hint: We have to find the area of the equilateral triangle whose side length is a. We start to solve the given question considering an equilateral triangle. Then, we find the length of the height and base of the equilateral triangle to compute area using the formula $\dfrac{1}{2}\times base\times height$

Complete step by step solution:
We are asked to find the area of the equilateral triangle whose side length is a. We will be solving the given question by finding out the length of the base and height of the equilateral triangle to find the area using the formula $\dfrac{1}{2}\times base\times height$
The equilateral triangle is a triangle in which all three sides have the same length.
According to our question,
All the sides of the given equilateral triangle are of length a.
Let us consider an equilateral triangle $\vartriangle ABC$
The triangle can be diagrammatically represented as follows,

Now, we need to divide the equilateral triangle into half to get two congruent right-angled triangles.
The triangle can be diagrammatically represented as follows,

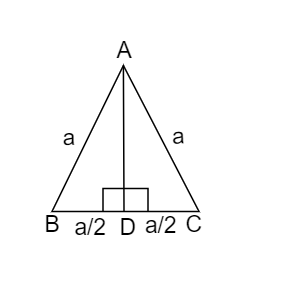
From the above, point D is the midpoint of the side BC.
From the figure, we know that $\vartriangle ABD$ is a right-angled triangle.
The length of the side $AD\;$can be found out using the Pythagoras theorem.
Pythagoras Theorem: 
This Theorem defines the relationship between the three sides of a triangle.
It states that the square of the hypotenuse of the right-angled triangle is equal to the sum of the squares of the other two sides of a triangle.
The other two sides of a triangle are designated as the base and height of a triangle respectively.
According to Pythagoras Theorem,
$\Rightarrow {{\left( hypotenuse \right)}^{2}}={{\left( base \right)}^{2}}+{{\left( height \right)}^{2}}\;$
Here,
$hypotenuse=AB=a$ ;
$base=BD=\dfrac{a}{2}$ ;
$height=AD$
Substituting the values in the Pythagoras theorem, we get,
$\Rightarrow {{\left( a \right)}^{2}}={{\left( \dfrac{a}{2} \right)}^{2}}+{{\left( AD \right)}^{2}}$
Expanding the squares, we get,
$\Rightarrow {{a}^{2}}=\dfrac{{{a}^{2}}}{4}+{{\left( AD \right)}^{2}}$
Shifting the term $\dfrac{{{a}^{2}}}{4}$ to the other side of the equation, we get,
$\Rightarrow {{a}^{2}}-\dfrac{{{a}^{2}}}{4}={{\left( AD \right)}^{2}}$
Taking LCM on the left-hand side, we get,
$\Rightarrow \dfrac{4{{a}^{2}}-{{a}^{2}}}{4}={{\left( AD \right)}^{2}}$
Simplifying the above equation, we get,
$\Rightarrow \dfrac{3{{a}^{2}}}{4}={{\left( AD \right)}^{2}}$
The above equation can also be written as follows,
$\Rightarrow {{\left( AD \right)}^{2}}=\dfrac{3{{a}^{2}}}{4}$
$\Rightarrow AD=\pm \sqrt{\dfrac{3{{a}^{2}}}{4}}$
Simplifying the above equation, we get,
$\Rightarrow AD=\pm \dfrac{\sqrt{3}a}{2}$
The height of the triangle can not be negative.
$\therefore AD=\dfrac{\sqrt{3}a}{2}$
From geometry,
We know that the area of the triangle is given as follows,
$\Rightarrow Area=\dfrac{1}{2}\times base\times height$
For the given equilateral triangle,
$base=BC=a$ ;
$height=AD=\dfrac{\sqrt{3}a}{2}$
Substituting the same, we get,
$\Rightarrow Area=\dfrac{1}{2}\times a\times \dfrac{\sqrt{3}a}{2}$
Simplifying the above equation, we get,
$\Rightarrow Area=\dfrac{\sqrt{3}{{a}^{2}}}{4}$

$\therefore$ The area of the equilateral triangle whose side length is a is given by $\dfrac{\sqrt{3}{{a}^{2}}}{4}$.

Note: We should remember that the value of $\sqrt{{{a}^{2}}}$ is not $+a$ but $\pm a$ . For any right-angled triangle, the hypotenuse is the length of the longest side of the triangle. Pythagoras theorem is valid only in the case of the right-angled triangle.