Question

What is the area of a right triangle if the radius of its circumcircle is 3 cm and altitude drawn to the hypotenuse is 2 cm?

a)$4\sqrt{3}c{{m}^{2}}$
b) $6c{{m}^{2}}$
c) $7c{{m}^{2}}$
d) $5c{{m}^{2}}$

Answer 1

Hint: Let ABC be the right triangle, with BO as altitude from vertex B on hypotenuse AC. As it is mentioned that a circle circumscribes the triangle ABC, therefore AC is the diameter of the circle, because an angle subtended by the diameter on the circle is always ${{90}^{\circ }}$. Also, we have a radius of the circle equal to 3 cm. So, we get the value of diameter. Now, in triangle ABC, we have base AC and height BO, so by using the formula $A=\dfrac{1}{2}\times base\times height$, find the area of the triangle.

Complete step-by-step solution:

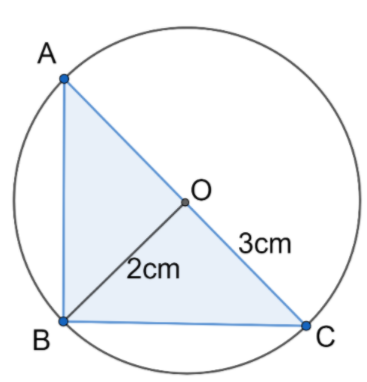
In the above figure, we have a circle with center O and radius OC equal to 3 cm that circumscribes a right triangle ABC.
As we know the diameter of a circle is twice its radius.
So, diameter of circle is:
 $\begin{align}
  & AC=2\times OC \\
 & =2\times 3 \\
 & =6\text{ }cm
\end{align}$
Now, in triangle, we have base AC = 6 cm and height BO = 2 cm
So, by using the formula $A=\dfrac{1}{2}\times base\times height$, we get area of triangle ABC as:
$\begin{align}
  & A=\dfrac{1}{2}\times 6\times 2 \\
 & =6\text{ }c{{m}^{2}}
\end{align}$
Hence, option (b) is the correct answer.

Note: A circumcircle is a unique circle that passes through all vertices (corner points) of a triangle. The center of the circumcircle is called the circumcentre, and the circle's radius is called the circumradius. For a right-angled triangle, the hypotenuse is the diameter of the circumcircle. Therefore, the midpoint of the triangle is the center of the circumcircle.