Question

What is the area of a right angled isosceles triangle whose hypotenuse is $6\sqrt 2 $cm?
$
  (a){\text{ 12c}}{{\text{m}}^2} \\
  (b){\text{ 18c}}{{\text{m}}^2} \\
  (c){\text{ 24c}}{{\text{m}}^2} \\
  (d){\text{ 36c}}{{\text{m}}^2} \\
 $

Answer 1

Hint: In this question put side AB=BC because it is a isosceles triangle and equate it to some variable, then use Pythagoras theorem which is ${\left( {{\text{base}}} \right)^2} + {\left( {{\text{perpendicular}}} \right)^2} = {\left( {{\text{hypotenuse}}} \right)^2}$ to get the variable and then the area.

Complete step-by-step answer:

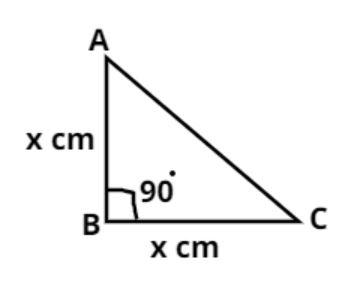
As we know in an isosceles triangle two sides are equal.

Now the given isosceles triangle is a right angle triangle. Therefore its base and perpendicular are equal as shown in figure.

Let its base and perpendicular be x cm.

Now it is given that its hypotenuse is AC = $6\sqrt 2 $ cm.

So apply Pythagoras theorem in right triangle we have,

$ \Rightarrow {\left( {{\text{base}}} \right)^2} + {\left( {{\text{perpendicular}}} \right)^2} =
{\left( {{\text{hypotenuse}}} \right)^2}$

Now substitute the values we have,

$ \Rightarrow {\left( x \right)^2} + {\left( x \right)^2} = {\left( {6\sqrt 2 } \right)^2}$

$ \Rightarrow 2{x^2} = 72$

Now divide by 2 we have,

\[ \Rightarrow {x^2} = \dfrac{{72}}{2} = 36 = {6^2}\]

Therefore x = 6 cm.

Now as we know that the area (A) of the triangle is half multiplied by base and
perpendicular.

$ \Rightarrow A = \dfrac{1}{2} \times x \times x$ $cm^2$.

Now substitute the value of x in this equation we have,

$ \Rightarrow A = \dfrac{1}{2} \times 6 \times 6 = 18$ $cm^2$.

So this is the required area of the right isosceles triangle.

Hence option (B) is correct.

Note: The important step in this question was the area formulation part of an isosceles triangle, as it does not differ from normal triangle as both are $\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$, however for an equilateral triangle in which all the three sides are equal the area is given as $\dfrac{{\sqrt 3 }}{4} \times {\text{sid}}{{\text{e}}^2}$.