Question

What are the ways of representing a relation?
$
  {\text{A}}{\text{. Set builder form}} \\
  {\text{B}}{\text{. Roster form}} \\
  {\text{C}}{\text{. Arrow diagram}} \\
  {\text{D}}{\text{. All of these}} \\
$

Answer 1

Hint: To solve this question we should have a good understanding of relation as well as set builder form, Roster form, arrow diagram and then we can be able to answer ways of representing a relation.

Complete step-by-step answer:
Relation: A relation between two sets is a collection of ordered pairs containing one object from each set. If the object x is from the first set and the object y is from the second set, then are objects said to be related if the ordered pair (x,y) is in the relation. A function is a type of relation.
Now we will understand the relation.
Set builder form: - Set builder notation is a shorthand used to write sets, often for sets with an infinite
Number of elements. It is used with common types of numbers, such as integers, real numbers and natural numbers. This notation can also be used to express sets with an interval or an equation.
Roster form: - Roster form or tabular form in this form all the elements of a set are listed, the elements are being separated by commas and are enclosed within braces $\left\{ {} \right\}$ . for example Z = the set of all integers $\left\{ { \ldots , - 3, - 2, - 1,0,1,2,3, \ldots } \right\}$ .
Arrow diagram: -
$ \Rightarrow $ Draw two circles representing set A and set B
$ \Rightarrow $ write their elements in the corresponding sets, that means elements of set A in circle A and elements of set B in circle B .
$ \Rightarrow $ Draw arrows from A to B which satisfy the relation and indicate the ordered pairs.
For example:
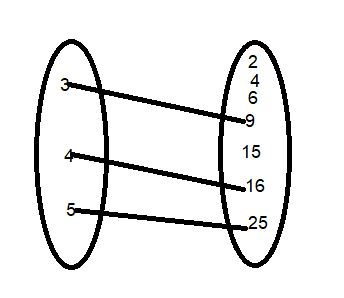
If A = $\left\{ {3,4,5} \right\}$ B = $\left\{ {2,4,6,9,15,16,25} \right\}$ then relation R from A to B is defined as ‘ is a positive square root of ‘ and can be represented by the arrow diagram as shown.
Here R = $\left\{ {\left( {3,9} \right),\left( {4,16} \right),\left( {5,25} \right)} \right\}$
In this form, the relation R from set A to set B is represented by drawing arrows from the first component to the second component of all ordered pairs which belong to R.

Note:- Whenever you get this type of question the key concept of solving is you have to understand all the terms like relation roster form set builder form and then we have to check that can we represent this relation in these forms or not .