Question

What are the possible expressions for the dimensions of the cuboids whose volume are given below?
i) Volume: $3{{x}^{2}}-12x$
ii) Volume: $12k{{y}^{2}}+8ky-20k$

Answer 1

Hint: First we will define what a cuboid and how its volume is calculated. Then after that we will factorize the volume given in question and compare with the formula of volume of the cuboid that is: $V=l\times b\times h\text{ }$, then we will write all the three dimensions separately.

Complete step by step answer:
As we know that a cuboid is a three dimensional structure having six rectangular faces. These six faces of the cuboid exist as a pair of three parallel faces, as shown in figure below:

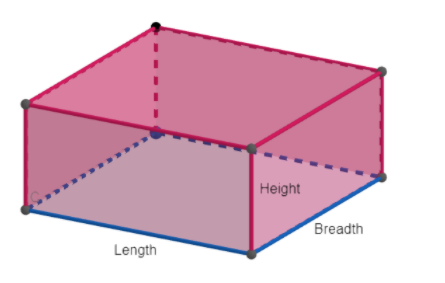
Now let’s consider where we need to calculate the amount of sand that can be filled in a cuboidal box that means we meant to calculate the capacity of this box. The capacity of the box is basically equal to the volume of cuboid involved. The volume of a cuboid is given by the product of its dimensions, that is:
$V=l\times b\times h\text{ }.......\text{Equation 1}$ , where $l$ = length, $b$ = breadth, $h$ = height.
Now we are given in the question that:
 i) Volume: $3{{x}^{2}}-12x$
Let’s start by factoring the above equation, we will take out $3x$ common and then we will get:$3x\left( x-4 \right)$ , this can be written as: $3\times x\times \left( x-4 \right)$
Hence, volume = $3\times x\times \left( x-4 \right)$ , we will compare it with equation 1 and therefore we will get the possible dimensions of the cuboid as follows:
$l$ = length = $3$ ,
$b$ = breadth = $x$ ,
$h$ = height = $x-4$ .

ii) Volume: $12k{{y}^{2}}+8ky-20k$
We will first take out $4k$ common out of the equation: $4k\left( 3{{y}^{2}}+2y-5 \right)$ , We will factorize the $\left( 3{{y}^{2}}+2y-5 \right)$ separately:
$\begin{align}
  & \left( 3{{y}^{2}}+2y-5 \right) \\
 & =3{{y}^{2}}+5y-3y-5 \\
 & =y\left( 3y+5 \right)-1\left( 3y+5 \right) \\
 & =\left( 3y+5 \right)\left( y-1 \right) \\
\end{align}$
Thus, $12k{{y}^{2}}+8ky-20k=4k\left( 3y+5 \right)\left( y-1 \right)$
So volume of the cuboid: $4k\times \left( 3y+5 \right)\times \left( y-1 \right)$ we will compare it with equation 1 and therefore we will get the possible dimensions of the cuboid as follows:
$l$ = length = $4k$ ,
$b$ = breadth = $3y+5$ ,
$h$ = height = $y-1$ .

So, the correct answer is “Option A”.

Note: For factorization first take the common variables and constant out and then look if it is a quadratic equation proceed with the middle term method, in which you have to find two numbers whose sum = b and the product is ac, where a,b, and c are coefficients of the quadratic equation: $a{{x}^{2}}+bx+c$.