Question

What are some examples of non-differentiable functions?

Answer 1

Hint: A function $ f(x) $ is said to be differentiable, if the derivative of the function exists at every point in its given domain. Geometrically the derivative of a function $ f(x) $ at a point $ x = {x_0} $ is defined as the slope of the graph of $ f(x) $ at $ x = {x_0} $ . Then the function is said to be non-differentiable if the derivative does not exist at any one point of its domain.

Complete step-by-step answer:
Some examples of non-differentiable functions are:
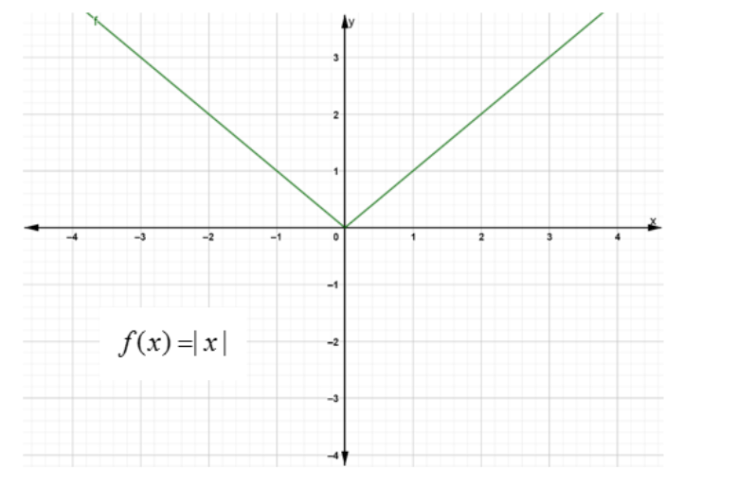
A function is non-differentiable when there is a cusp or a corner point in its graph. For example consider the function $ f(x) = |x| $ , it has a cusp at $ x = 0 $ hence it is not differentiable at $ x = 0 $ .

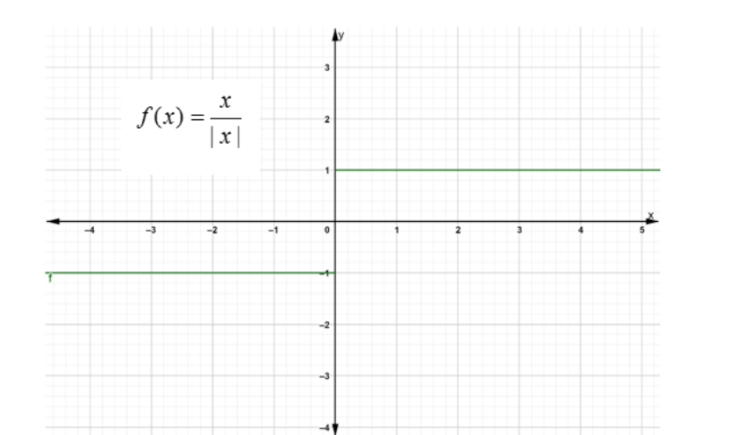
If the function is not continuous then it is not differentiable, i.e. when there is a gap or a jump in the graph of the function then it is not continuous hence not differentiable. For example consider the step function $ f(x) = \dfrac{x}{{|x|}} $ , here there is a jump discontinuity $ x = 0 $ .


                               

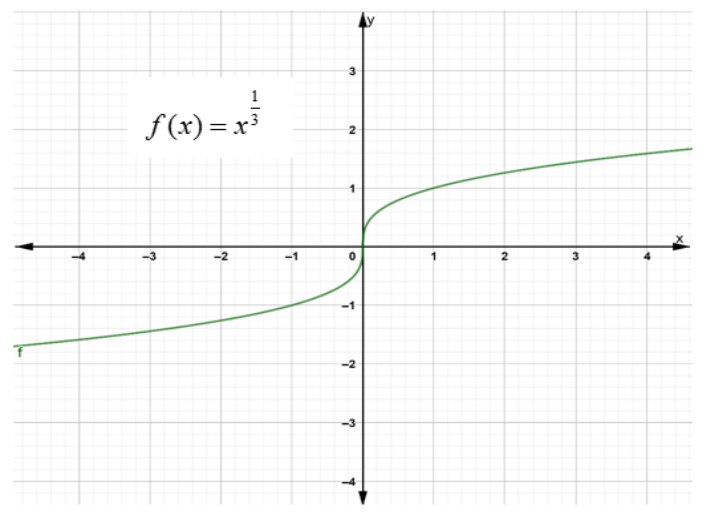
If the function can be defined but its derivative is infinite at a point then it becomes non-differentiable. This happens when there is a vertical tangent line at that point. For example, consider $ f(x) = {x^{\dfrac{1}{3}}} $ , it has a vertical tangent line at $ x = 0 $ , therefore at $ x = 0 $ its derivative is infinite.

    

When the function is unbounded and goes to infinity at some point of its domain it becomes non-differentiable. For example consider $ f(x) = \dfrac{1}{x} $ which goes to infinity at $ x = 0 $ , hence non- differentiable

Note: If a function is differentiable then it is always continuous but the converse need not be true, i.e. there are functions which are continuous but not differentiable for example $ f(x) = |x| $ is continuous at $ x = 0 $ but not differentiable at $ x = 0 $ . By studying the graph of the given function we can easily conclude about the continuity and differentiability of the function.