Question

AP = 3cm, BP = 3cm, AQ = 4cm then find CQ.

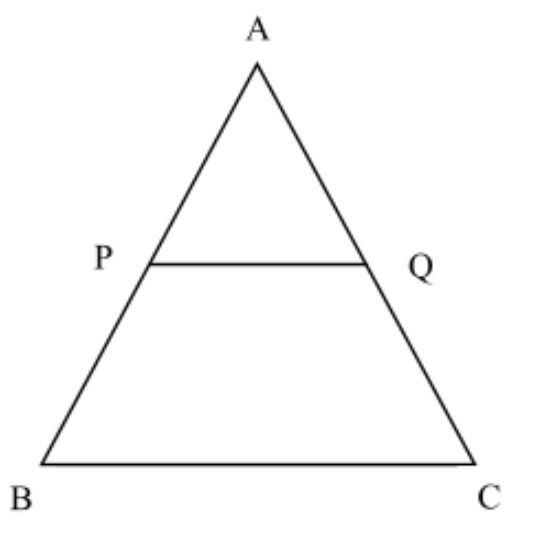
Answer 1

Hint: As we know that there are many theorems for solving the problems related to triangles. We will solve this question using the ‘Triangle Proportionality Theorem’ which states that if a line is parallel to one side of a triangle intersects the other two sides, then it divides those sides into proportional segments.
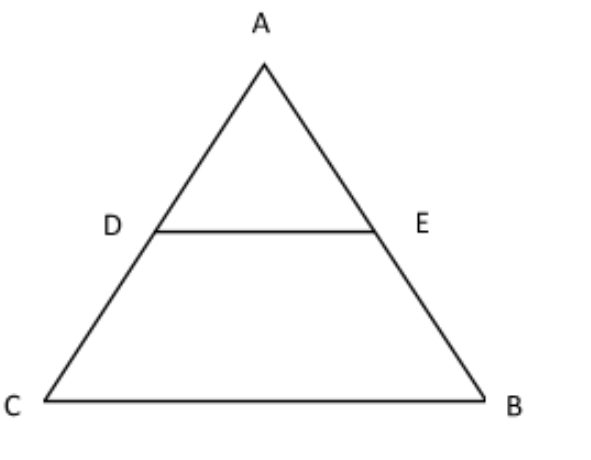
This is also called the “Side-Splitting Theorem” because the mid-segment splits the sides that it intersects. In $\Delta ABC{\text{ with }}\overline {DE} \parallel \overline {CB} $
$\therefore \dfrac{{CD}}{{DA}} = \dfrac{{BE}}{{EA}}$

Complete step-by-step answer:
Given that:
AP=2cm
BP=3cm
AQ=4cm
By using Side-Splitting Theorem,
$\begin{gathered}
  \dfrac{{BP}}{{AP}} = \dfrac{{CQ}}{{AQ}} \\
  \dfrac{3}{2} = \dfrac{x}{4} \\
  x = \dfrac{{3 \times 4}}{2} \\
  x = \dfrac{{12}}{2} \\
  x = 6cm \\
\end{gathered} $
$\therefore x = CQ = 6cm$

Note:1) Students must keep in mind that we can use the Side-Splitter Theorem only for the four segments on the split sides of the triangle. The side splitter theorem is a natural extension of similarity ratio, and it happens any time that a pair of parallel lines intersects a triangle. Do not use it for the parallel sides, which are in a different ratio. The Side-Splitter only applies to the intercepted sides. It does not apply to the bottoms.
2) When you move the parallel line, you are changing the proportion between the upper and lower segments. When you move the point, the segments may get longer or shorter, but the proportion stays the same.
3) A corollary of this theorem is that when three parallel lines intersect two transversals, then the segments intercepted on the transversal are proportional.
4) Students will be able to use proportional relationships in triangles. Students will discover that proportional relationships can be set up in multiple ways. Students will use proportional relationships of three parallel lines cut by two transversals.