Question

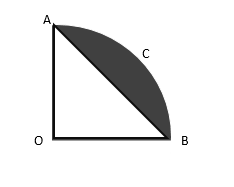
AOBC is a quadrant of a circle of a radius 10m. Calculate the area of the Shaded Portion.

Answer 1

Hint:The area of the shaded region is the difference between the area of the entire polygon and the area of the unshaded part inside the polygon.
The area of the shaded part can occur in two ways in polygons. The shaded region can be located at the center of a polygon or at the sides of the polygon.
As stated before, the area of the shaded region is calculated by taking the difference between the area of an entire polygon and the area of the unshaded region.
Area of shaded region = area of outer shape – area of the unshaded inner shape


Complete Step-by-step explanation:
Here radius of quadrant circle (R) = 10 m
Area of quadrant circle (AOBC) = \[\dfrac{1}{4} \times \pi \times {R^2}\] ...1)
 Area of right-angle triangle (AOB)
= \[\dfrac{1}{2} \times OA \times OB\]
= \[\dfrac{1}{2} \times R \times R\]
  So
  Area of right-angle triangle (AOB)
= \[\dfrac{1}{2} \times R \times R = \dfrac{1}{2} \times {R^2}\] ...2)
 Area of shaded portion = Area of quadrant circle (AOBC) - Area of right-angle triangle (AOB) ...3)
So, from equation 1), equation 2) and equation 3) it can be written as
  Area of shaded portion
= \[\left( {\dfrac{1}{4} \times \pi \times {R^2}} \right) - \left( {\dfrac{1}{2} \times {R^2}} \right)\]

 Area of shaded portion= \[\dfrac{1}{2} \times {R^2} \times \left[ {\dfrac{\pi }{2} - 1} \right]\] ...4)
 After putting the value in equation 4)
 Area of shaded portion \[\dfrac{1}{2} \times {10^2} \times \left[ {\dfrac{\pi }{2} - 1} \right] = 28.57\,{m^2}\]


Note:Students should keep in mind the area of circle = \[\pi \times {R^2}\]and area of triangle = \[\dfrac{1}{2} \times height \times base\].
 The area of the shaded region is calculated by taking the difference between the area of an entire quadrant of the circle and the area of the unshaded region which is right- angle triangle for this case.
Area of shaded region = area of outer shape – area of the unshaded inner shape