Question

Answer the following questions:
(a) Time period of a particle in SHM depends on the force constant k and mass m of the particle:
 $ T=2\pi \sqrt{\dfrac{m}{k}} $. A simple pendulum executes SHM approximately. Why then is the time period of the pendulum independent of mass of the pendulum?
(b) The motion of a simple pendulum is approximately simple harmonic for small angle oscillations. For a larger angle of oscillation a more involved analysis shows that T is greater than 2πgl​​. Think of a qualitative argument to appreciate this result.
(c) A man with a wristwatch on his hand falls from the top of a tower. Does the
watch give correct time during the free fall?
(d) What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity?

Answer 1

Hint: This case is the situation of a simple pendulum in SHM. The formula for the time period is given to us in the part a of the question which will be helpful throughout the question. For the b part, the key concept will be, \[sin\theta ~\approx \theta \]. Also, for the c part, remember that in a free fall, the gravity disappears.

Complete step-by-step answer:
(a) For a simple pendulum, the force constant or spring factor k is equal to the mass m; thus, both in the denominator and in the numerator, m cancels out. That is why the length of time of the simple pendulum is different from the mass of the bob.
Let us take a look at this with the help of formula
 $ T=2\pi \sqrt{\dfrac{m}{k}} $
Now,
For a spring,
F = -kx
So,
 $ \Rightarrow k=-\dfrac{F}{x} $
 $ \Rightarrow k=\dfrac{mg}{L} $
Using the above value in the formula, we have
 $ \Rightarrow T=2\pi \sqrt{\dfrac{m}{\dfrac{mg}{L}}} $
 $ \Rightarrow T=2\pi \sqrt{\dfrac{L}{g}} $
Hence proved.

(b) For a small angle of \[sin\theta ~\approx \theta \], but for a wide angle of \[sin\theta <\theta \]. Since this vector is compounded, \[mgsin\theta \] is replaced by \[mg\theta \] with the restored power. This suggests an efficient reduction in g for large angles.
Consequently, an improvement in time duration T over that given by
 \[T\text{ }=\text{ }2\pi \sqrt{\dfrac{L}{g}}\]
Compare it to the situation in which sin is presumed \[sin\theta ~=\theta \]
F= \[-mg\sin \theta \] where,
F= Restoring force
m= Mass of the bob
g = Acceleration due to gravity
 \[\theta \] = Angle of displacement
For small  \[\theta \], \[sin\theta \simeq \theta \]
For large \[\theta \],   \[\sin \theta \]  is greater than  \[\theta \].
This decreases the effective value of g.

(c) Indeed, because the operation of the wrist watch depends on the movement of the spring and is not affected by gravity. Since, the needles of the wristwatch moves due to the constant force applied by the spring (machine), it can not be said to be executing SHM, even after constant time period

(d) For an object that is in free fall, gravity disappears, so the frequency is zero.

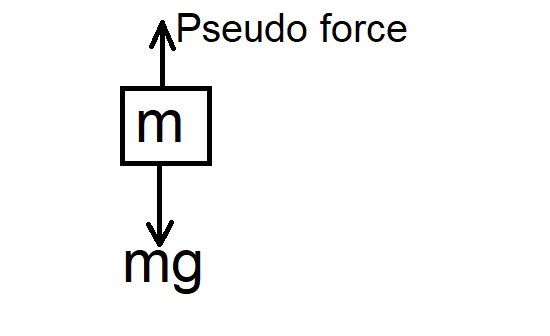
Here,
Pseudo force = mg
Hence the two forces cancel out each other

Note: The only force acting on the body when in free fall is the force of gravity-a non-contact force. Without any other competing forces, because the force of gravity can not be sensed, you will have no understanding of it. When you are in a state of free fall, you can feel weightless.