Question

Answer the following question in one word or one sentence or as per exact requirement of the question.
If A = {(x, y): y =${{\text{e}}^{\text{x}}}$, x ϵ R} and B = {(x, y): y =${{\text{e}}^{{\text{ - x}}}}$, x ϵ R}, then write A ∩ B.

Answer 1

Hint: To determine the answer, we write the definition of A ∩ B using the given A and B. Then we perform the calculations to get the values of x and y. Definition of A ∩ B states that the set of elements which are common in both sets A and B.

Complete step-by-step solution -

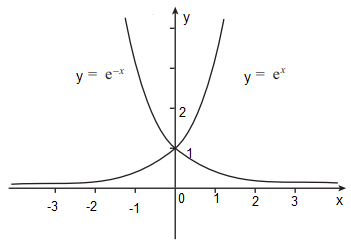
We need: A ∩ B
⟹ {(x, y): y =${{\text{e}}^{\text{x}}}$, x ϵ R} ∩ {(x, y): y =${{\text{e}}^{{\text{ - x}}}}$, x ϵ R}
⟹ {(x, y): y =${{\text{e}}^{\text{x}}}$∩ ${{\text{e}}^{{\text{ - x}}}}$, x ϵ R}
The intersection of ${{\text{e}}^{\text{x}}}$and ${{\text{e}}^{{\text{ - x}}}}$is nothing but,
⟹${{\text{e}}^{\text{x}}}$=${{\text{e}}^{{\text{ - x}}}}$
Applying ln on both sides we get,
⟹ln ${{\text{e}}^{\text{x}}}$= ln ${{\text{e}}^{{\text{ - x}}}}$
We know ln (${{\text{e}}^{\text{x}}}$) = x ln e = x (1) = x -- ln (e) = 1, logarithmic identity.
⟹x = -x
⟹2x = 0
⟹x = 0
Therefore, ${{\text{e}}^{\text{x}}}$= ${{\text{e}}^{{\text{ - x}}}}$= ${{\text{e}}^0}$= 1
Hence y = 1.
At x = 0, y = 1
Therefore, A ∩ B = {(0, 1)} is a singleton set.

Note: The key in such problems is to understand the definition of A ∩ B using the given A and B. A intersection B refers to a common solution set of A and B. Using the correct operations, like applying the log function to reduce the equations and finding the values of x and y is a crucial step.
Any number to the power of 0 is 1. e is a numerical constant with a value of 2.71828.