
Answer all the following question:
1) State Gauss’ law in electrostatics
2) Write the color code for carbon resistance $47k\Omega \pm 10%$.
3) How the frequency of revolution of a charged particle in a magnetic field depends on its speed?
4) What is the significance of Lenz’s law.
Answer
564.3k+ views
Hint: These are individual short questions. These are informative questions. We need to go through the information to answer them. We need to know about Gauss’ theorem, color codes of resistances, the expression for the frequency of a charged particle in a magnetic field, and Lenz’s law. Let’s solve it one by one.
Formula used:
$1){{\Phi}_{E}}=\oint{\overrightarrow{E}.\overrightarrow{dA}=\dfrac{q}{{{\varepsilon }_{0}}}}$
$3)n=\dfrac{qB}{2\pi m}$
$4)\varepsilon =-N\dfrac{d{{\phi }_{B}}}{dt}$
Complete step-by-step solution
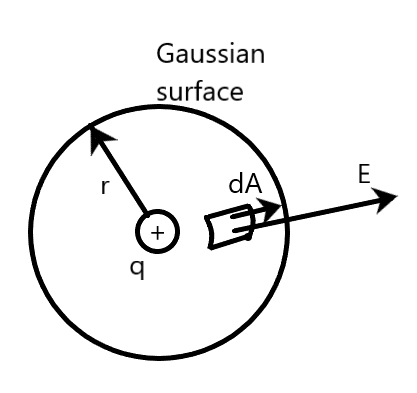
1) Gauss’ theorem states that the electric flux ${{\Phi }_{E}}$ through any closed surface is equal to $\dfrac{1}{{{\varepsilon }_{0}}}$ times the net charge $q$ enclosed by the surface. i.e.
${{\Phi }_{E}}=\oint{\overrightarrow{E}.\overrightarrow{dA}=\dfrac{q}{{{\varepsilon }_{0}}}}$
2) From the table (which shows color codes for resistors) given below, it is clear that $4=$ yellow, $7=$ violet,${10}^{3} =$ orange will give $47\times {{10}^{3}}$ $\Omega $ .The silver band gives tolerance of $10$% . Thus, the color code for $47k\Omega \pm 10$% is in the order of yellow, violet, orange and silver.
3) If the charge and mass of the particle are $q$ and $m$ respectively and if the magnetic field is $B$ , then, we know that the frequency $(n)$ of the particle is given by:
$n=\dfrac{qB}{2\pi m}$
Clearly, frequency of the particle is independent of the speed of the particle. If the speed of the particle increases, its radius also increases so that the time taken to complete one revolution remains the same.
4) Lenz’s law states that the direction of the induced emf, or the current in any circuit is such that it opposes the cause that produces it. Mathematically, this is represented as:
$\varepsilon =-N\dfrac{d{{\phi }_{B}}}{dt}$
where
$\varepsilon $ is the induced emf
$N$ is the number of turns in the coil used in the circuit
$\dfrac{d{{\phi }_{B}}}{dt}$ is the change in magnetic flux with respect to time
Here, negative sign indicates that the induced emf is opposite to the change in magnetic flux that causes it.
This law is in agreement with the law of conservation of energy. Because to produce any induced emf or current, we have to work against something and that work gets transformed into the induced emf or current. If it would have been not so, without doing any work we would have got induced emf or current which is gross violation of law of conservation of energy. This is the significance of Lenz’s law.
Note: It is important that we remember many relations to answer all these questions at a time. Like in the case of the color code, we have to remember different color codes, which can easily be derived from the table, provided we remember it thoroughly. Similarly, we need to remember expressions for Gauss law, Lenz law as well as the expression for frequency of a charged particle in a magnetic field.
Formula used:
$1){{\Phi}_{E}}=\oint{\overrightarrow{E}.\overrightarrow{dA}=\dfrac{q}{{{\varepsilon }_{0}}}}$
$3)n=\dfrac{qB}{2\pi m}$
$4)\varepsilon =-N\dfrac{d{{\phi }_{B}}}{dt}$
Complete step-by-step solution
1) Gauss’ theorem states that the electric flux ${{\Phi }_{E}}$ through any closed surface is equal to $\dfrac{1}{{{\varepsilon }_{0}}}$ times the net charge $q$ enclosed by the surface. i.e.
${{\Phi }_{E}}=\oint{\overrightarrow{E}.\overrightarrow{dA}=\dfrac{q}{{{\varepsilon }_{0}}}}$

2) From the table (which shows color codes for resistors) given below, it is clear that $4=$ yellow, $7=$ violet,${10}^{3} =$ orange will give $47\times {{10}^{3}}$ $\Omega $ .The silver band gives tolerance of $10$% . Thus, the color code for $47k\Omega \pm 10$% is in the order of yellow, violet, orange and silver.
| Colour | Digit | Multiplier | Tolerance |
| Black | 0 | \[{{10}^{0}}=1\] | |
| Brown | 1 | ${{10}^{1}}=10$ | |
| Red | 2 | ${{10}^{2}}$ | |
| Orange | 3 | ${{10}^{3}}$ | |
| Yellow | 4 | ${{10}^{4}}$ | |
| Green | 5 | ${{10}^{5}}$ | |
| Blue | 6 | ${{10}^{6}}$ | |
| Violet | 7 | ${{10}^{7}}$ | |
| Grey | 8 | ${{10}^{8}}$ | |
| White | 9 | ${{10}^{9}}$ | |
| Gold | - | $0.1$ | $\pm 5%$ |
| Silver | - | $0.01$ | $\pm 10%$ |
| No Colour | - | - | $\pm 20%$ |
3) If the charge and mass of the particle are $q$ and $m$ respectively and if the magnetic field is $B$ , then, we know that the frequency $(n)$ of the particle is given by:
$n=\dfrac{qB}{2\pi m}$
Clearly, frequency of the particle is independent of the speed of the particle. If the speed of the particle increases, its radius also increases so that the time taken to complete one revolution remains the same.
4) Lenz’s law states that the direction of the induced emf, or the current in any circuit is such that it opposes the cause that produces it. Mathematically, this is represented as:
$\varepsilon =-N\dfrac{d{{\phi }_{B}}}{dt}$
where
$\varepsilon $ is the induced emf
$N$ is the number of turns in the coil used in the circuit
$\dfrac{d{{\phi }_{B}}}{dt}$ is the change in magnetic flux with respect to time
Here, negative sign indicates that the induced emf is opposite to the change in magnetic flux that causes it.
This law is in agreement with the law of conservation of energy. Because to produce any induced emf or current, we have to work against something and that work gets transformed into the induced emf or current. If it would have been not so, without doing any work we would have got induced emf or current which is gross violation of law of conservation of energy. This is the significance of Lenz’s law.
Note: It is important that we remember many relations to answer all these questions at a time. Like in the case of the color code, we have to remember different color codes, which can easily be derived from the table, provided we remember it thoroughly. Similarly, we need to remember expressions for Gauss law, Lenz law as well as the expression for frequency of a charged particle in a magnetic field.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




