Question

Angle of semicircle is:
A.$60^\circ $
B.$90^\circ $
C.$180^\circ $
D.$360^\circ $

Answer 1

Hint: Using the property of a circle, the angle subtended by an arc at the center is double the angle subtended by it on any point on the remaining part of the circle.

Complete step-by-step answer:
According to question, the figure can be drawn as shown-

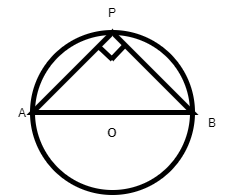
Here, AOB is a straight line passing through center O.
$\therefore $ Angle subtended by the arc AB at origin O is
$\angle AOB = 180^\circ $
The angle subtended by an arc at the center is double the angle subtended by it on any point on the remaining part of the circle.
$\therefore \angle AOB = 2\angle APB$
$\dfrac{{\angle AOB}}{2} = \angle APB$
$\dfrac{{180^\circ }}{2} = \angle APB$
$\angle APB = 90^\circ $
Hence, it can be said that the angle of a semicircle is a right angle.
Note: For solving problems related to angles subtended by an arc in a circle, we need to draw the diagram and then use the property of angles subtended by an arc in a circle. Also, Angle subtended by any straight line is 180°.